
 
A convolution is an integral that expresses the amount of overlap of one function 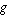 as it is shifted over another function as it is shifted over another function 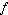 . It therefore "blends"
one function with another. For example, in synthesis imaging . It therefore "blends"
one function with another. For example, in synthesis imaging  , the measured dirty
map , the measured dirty
map  is a convolution of the "true" CLEAN map is a convolution of the "true" CLEAN map  with the dirty beam with the dirty beam  (the Fourier transform of the sampling distribution). The convolution
is sometimes also known by its German name, faltung ("folding"). (the Fourier transform of the sampling distribution). The convolution
is sometimes also known by its German name, faltung ("folding").
Abstractly, a convolution is defined as a product of functions 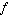 and and  that are objects
in the algebra of Schwartz functions
in that are objects
in the algebra of Schwartz functions
in 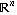 . Convolution of two functions . Convolution of two functions 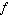 and and 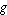 over a finite range over a finite range
![[0,t]](Convolution_files/inline8.gif) is given by is given by
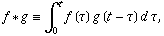 | (1) |
where the symbol 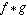 (occasionally also written
as (occasionally also written
as 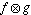 ) denotes convolution of ) denotes convolution of 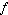 and and 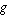 . Convolution is
more often taken over an infinite range, . Convolution is
more often taken over an infinite range,
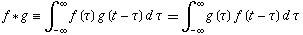 | (2) |
(Bracewell 1999, p. 25).
The animations above graphically illustrate the convolution of two rectangle functions (left) and two Gaussians (right). In the plots, the green curve shows the
convolution of the blue and red curves as a function of  , the position indicated
by the vertical green line. The gray region indicates the product , the position indicated
by the vertical green line. The gray region indicates the product 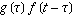 as
a function of as
a function of 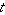 , so its area as a function of , so its area as a function of 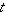 is precisely the
convolution. is precisely the
convolution.
The convolution of two rectangle functions 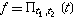 and
and 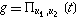 has the particularly
simple form has the particularly
simple form
![f*g==[(t-t_1-u_1)Pi(t-t_1-u_1)-(t-t_2-u_1)Pi(t-t_2-u_1)-(t-t_1-u_2)Pi(t-t_1-u_2)+(t-t_2-u_2)Pi(t-t_2-u_2)].](Convolution_files/equation3.gif) | (3) |
Even more amazingly, the convolution of two Gaussians 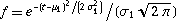 and
and 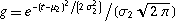 is another Gaussian
is another Gaussian
![f*g==1/(sqrt(2pi(sigma_1^2+sigma_2^2)))e^(-[t-(mu_1+mu_2)]^2/[2(sigma_1^2+sigma_2^2)]).](Convolution_files/equation4.gif) | (4) |
Let 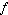 , , 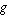 , and , and 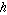 be arbitrary functions
and be arbitrary functions
and  a constant. Convolution satisfies the properties a constant. Convolution satisfies the properties
(Bracewell 1999, p. 27), as well as
 | (8) |
Taking the derivative of a convolution
gives
 | (9) |
The area under a convolution is the product
of areas under the factors,
The horizontal function centroids
add
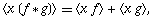 | (13) |
as do the variances
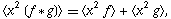 | (14) |
where
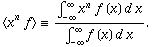 | (15) |
There is also a definition of the convolution which arises in probability theory and is given by
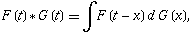 | (16) |
where 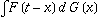 is a Stieltjes integral. is a Stieltjes integral.

Bracewell, R. "Convolution" and "Two-Dimensional Convolution." Ch. 3 in The Fourier Transform and Its Applications, 3rd ed. New
York: McGraw-Hill, pp. 25-50 and 243-244, 1999.
Hirschman, I. I. and Widder, D. V. The Convolution Transform. Princeton, NJ: Princeton University
Press, 1955.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill,
pp. 464-465, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Convolution and Deconvolution Using the FFT." §13.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing,
2nd ed. Cambridge, England: Cambridge University Press, pp. 531-537, 1992.
Weisstein, E. W. "Books about Convolution." http://www.ericweisstein.com/encyclopedias/books/Convolution.html.
|