Common Names: Adaptive thresholding, Dynamic thresholding
Thresholding is used to segment an image by setting all pixels whose intensity values are above a threshold to a foreground value and all the remaining pixels to a background value.
Whereas the conventional thresholding operator uses a global threshold for all pixels, adaptive thresholding changes the threshold dynamically over the image. This more sophisticated version of thresholding can accommodate changing lighting conditions in the image, e.g. those occurring as a result of a strong illumination gradient or shadows.
Adaptive thresholding typically takes a grayscale or color image as input and, in the simplest implementation, outputs a binary image representing the segmentation. For each pixel in the image, a threshold has to be calculated. If the pixel value is below the threshold it is set to the background value, otherwise it assumes the foreground value.
There are two main approaches to finding the threshold: (i) the
Chow and
Kaneko approach and
(ii) local
thresholding. The
assumption behind both methods is that smaller
image regions are more
likely to have approximately uniform
illumination, thus being more
suitable for thresholding.
Chow and Kaneko divide an image into an array of overlapping subimages and then find the optimum threshold for each subimage by investigating its histogram. The threshold for each single pixel is found by interpolating the results of the subimages. The drawback of this method is that it is computational expensive and, therefore, is not appropriate for real-time applications.
An alternative approach to finding the local threshold is to statistically examine the intensity values of the local neighborhood of each pixel. The statistic which is most appropriate depends largely on the input image. Simple and fast functions include the mean of the local intensity distribution,
the median value,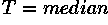 
or the mean of the minimum and maximum values,
The size of the neighborhood has to be large enough to cover sufficient foreground and background pixels, otherwise a poor threshold is chosen. On the other hand, choosing regions which are too large can violate the assumption of approximately uniform illumination. This method is less computationally intensive than the Chow and Kaneko approach and produces good results for some applications.
Like global thresholding, adaptive thresholding is used to separate desirable foreground image objects from the background based on the difference in pixel intensities of each region. Global thresholding uses a fixed threshold for all pixels in the image and therefore works only if the intensity histogram of the input image contains neatly separated peaks corresponding to the desired subject(s) and background(s). Hence, it cannot deal with images containing, for example, a strong illumination gradient.
Local adaptive thresholding, on the other hand, selects an individual threshold for each pixel based on the range of intensity values in its local neighborhood. This allows for thresholding of an image whose global intensity histogram doesn't contain distinctive peaks.
A task well suited to local adaptive thresholding is in segmenting text from the image
Because this image contains a strong illumination gradient, global thresholding produces a very poor result, as can be seen in
Using the mean of a 7eighborhood, adaptive thresholding yields
The method succeeds in the area surrounding the text because there are enough foreground and background pixels in the local neighborhood of each pixel; i.e. the mean value lies between the intensity values of foreground and background and, therefore, separates easily. On the margin, however, the mean of the local area is not suitable as a threshold, because the range of intensity values within a local neighborhood is very small and their mean is close to the value of the center pixel.
The situation can be improved if the threshold employed is not the mean, but (mean-C), where C is a constant. Using this statistic, all pixels which exist in a uniform neighborhood (e.g. along the margins) are set to background. The result for a 7eighborhood and C=7 is shown in
and for a 75neighborhood and C=10 in
The larger window yields the poorer result, because it is more adversely affected by the illumination gradient. Also note that the latter is more computationally intensive than thresholding using the smaller window.
The result of using the median instead of the mean can be seen in
(The neighborhood size for this example is 7nd C = 4). The result shows that, in this application, the median is a less suitable statistic than the mean.
Consider another example image containing a strong illumination gradient
This image can not be segmented with a global threshold, as shown in
where a threshold of 80 was used. However, since the image contains a large object, it is hard to apply adaptive thresholding, as well. Using the (mean - C) as a local threshold, we obtain
with a 7indow and C = 4, and
with a 140 window and C = 8. All pixels which belong to the object but do not have any background pixels in their neighborhood are set to background. The latter image shows a much better result than that achieved with a global threshold, but it is still missing some pixels in the center of the object. In many applications, computing the mean of a neighborhood (for each pixel!) whose size is of the order 140 may take too much time. In this case, the more complex Chow and Kaneko approach to adaptive thresholding would be more successful.
If your image processing package does not contain an adaptive threshold operator, you can simulate the effect with the following steps:
You can interactively experiment with this operator by clicking here.
why does the mean produce a better result than the median? Can you think of any example where the median is more appropriate?
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, pp 91 - 96.
R. Gonzales and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, pp 443 - 452.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1986, p 408.
C.K. Chow and T. Kaneko Automatic Boundary Detection of the Left Ventricle from Cineangiograms, Comp. Biomed. Res.(5), 1972, pp. 388-410.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
3
R. Fisher, S. Perkins, A. Walker and E. Wolfart.
