




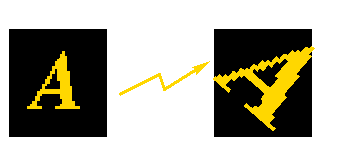
In many imaging systems, detected images are subject to geometric distortion introduced by perspective irregularities wherein the position of the camera(s) with respect to the scene alters the apparent dimensions of the scene geometry. Applying an affine transformation to a uniformly distorted image can correct for a range of perspective distortions by transforming the measurements from the ideal coordinates to those actually used. (For example, this is useful in satellite imaging where geometrically correct ground maps are desired.)
An affine transformation is an important class of linear 2-D geometric
transformations which maps variables (e.g. pixel intensity values
located at position 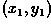 in an input image) into new variables
(e.g.
in an input image) into new variables
(e.g. 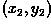 in an output image) by applying a linear combination
of translation, rotation,
scaling and/or shearing (i.e. non-uniform scaling in some
directions) operations.
in an output image) by applying a linear combination
of translation, rotation,
scaling and/or shearing (i.e. non-uniform scaling in some
directions) operations.
In order to introduce the utility of the affine transformation, consider the image
wherein a machine part is shown lying in a fronto-parallel plane. The circular hole of the part is imaged as a circle, and the parallelism and perpendicularity of lines in the real world are preserved in the image plane. We might construct a model of this part using these primitives; however, such a description would be of little use in identifying the part from
Here the circle is imaged as an ellipse, and orthogonal world lines are not imaged as orthogonal lines.
This problem of perspective can be overcome if we construct a shape description which is invariant to perspective projection. Many interesting tasks within model based computer vision can be accomplished without recourse to Euclidean shape descriptions (i.e. those requiring absolute distances, angles and areas) and, instead, employ descriptions involving relative measurements (i.e. those which depend only upon the configuration's intrinsic geometric relations). These relative measurements can be determined directly from images. Figure 1 shows a hierarchy of planar transformations which are important to computer vision.
Figure 1 Hierarchy of plane to plane transformation fromEuclidean (where only rotations and translations are allowed) to Projective (where a square can be transformed into any more general quadrilateral where no 3 points are collinear). Note that transformations lower in the table inherit the invariants of those above, but because they possess their own groups of definitive axioms as well, the converse is not true.
The transformation of the part face shown in the example image above is approximated by a planar affine transformation. (Compare this with the image
where the distance to the part is not large compared with its depth and, therefore, parallel object lines begin to converge. Because the scaling varies with depth in this way, a description to the level of projective transformation is required.) An affine transformation is equivalent to the composed effects of translation, rotation, isotropic scaling and shear.
The general affine transformation is commonly written in homogeneous coordinates as shown below:
By defining only the B matrix, this transformation can carry out pure translation:
Pure rotation uses the A matrix and is defined as (for positive angles being clockwise rotations):
Here, we are working in image coordinates, so the y axis goes downward. Rotation formula can be defined for when the y axis goes upward.
Similarly, pure scaling is:
(Note that several different affine transformations are often combined to produce a resultant transformation. The order in which the transformations occur is significant since a translation followed by a rotation is not necessarily equivalent to the converse.)
Since the general affine transformation is defined by 6 constants, it is
possible to define this transformation by specifying the new output
image locations 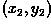 of any three input image coordinate
of any three input image coordinate
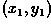 pairs. (In practice, many more points are measured and a
least squares method is used to find the best fitting transform.)
pairs. (In practice, many more points are measured and a
least squares method is used to find the best fitting transform.)
Most implementations of the affine operator allow the user to define a
transformation by specifying to where 3 (or less) coordinate pairs
from the input image 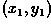 re-map in the output
image
re-map in the output
image 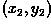 . (It is often the case, as with the
implementation used here, that the user is restricted to re-mapping
corner coordinates of the input image to arbitrary new
coordinates in the output image.) Once the transformation has been
defined in this way, the re-mapping proceeds by calculating, for each
output pixel location
. (It is often the case, as with the
implementation used here, that the user is restricted to re-mapping
corner coordinates of the input image to arbitrary new
coordinates in the output image.) Once the transformation has been
defined in this way, the re-mapping proceeds by calculating, for each
output pixel location 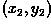 , the corresponding
input coordinates
, the corresponding
input coordinates 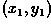 . If that input point is
outside of the image, then the output pixel is set to the background
value. Otherwise, the value of (i) the input pixel itself, (ii) the
neighbor nearest to the desired pixel position, or (iii) a bilinear
interpolation of the neighboring four pixels is used.
. If that input point is
outside of the image, then the output pixel is set to the background
value. Otherwise, the value of (i) the input pixel itself, (ii) the
neighbor nearest to the desired pixel position, or (iii) a bilinear
interpolation of the neighboring four pixels is used.
We will illustrate the operation of the affine transformation by applying a series of special-case transformations (e.g. pure translation, pure rotation and pure scaling) and then some more general transformations involving combinations of these.
Starting with the 256×256 binary artificial image
we can apply a translation using the affine operator in order to obtain the image
In order to perform
this pure translation, we define a transformation by re-mapping a
single point (e.g. the input image lower-left corner 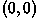 ) to a new position at
) to a new position at
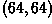 .
.
A pure rotation requires re-mapping the position of two corners to new
positions. If we specify that the lower-left corner moves to
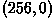 and the lower-right corner moves to
and the lower-right corner moves to
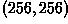 , we obtain
, we obtain
Similarly, reflection can be achieved by swapping the coordinates of two opposite corners, as shown in
Scaling can also be applied by re-mapping just two
corners. For example, we can send the lower-left corner to
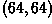 , while pinning the upper-right
corner down at
, while pinning the upper-right
corner down at 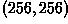 , and thereby
uniformly shrink the size of the image subject by a quarter, as shown
in
, and thereby
uniformly shrink the size of the image subject by a quarter, as shown
in
Note that here we have also translated the image. Re-mapping any 2 points can introduce a combination of translation, rotation and scaling.
A general affine transformation is specified by re-mapping 3
points. If we re-map the input image so as to move the lower-left
corner up to 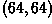 along the 45 degree
oblique axis, move the upper-right corner down by the same amount along
this axis, and pin the lower-right corner in place, we obtain an image
which shows some shearing effects
along the 45 degree
oblique axis, move the upper-right corner down by the same amount along
this axis, and pin the lower-right corner in place, we obtain an image
which shows some shearing effects
Notice how parallel lines remain parallel, but perpendicular corners are distorted.
Affine transformations are most commonly applied in the case where we
have a detected image which has undergone some type of distortion. The
geometrically correct version of the input image can be obtained from
the affine transformation by re-sampling the input image such
that the information (or intensity) at each point 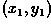 is mapped to the correct position
is mapped to the correct position 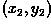 in a corresponding output image.
in a corresponding output image.
One of the more interesting applications of this technique is in remote sensing. However, because most images are transformed before they are made available to the image processing community, we will demonstrate the affine transformation with the terrestrial image
which is a contrast-stretched (cutoff fraction = 0.9) version of
We might want to transform this image so as to map the door frame back into a rectangle. We can do this by defining a transformation based on a re-mapping of the (i) upper-right corner to a position 30% lower along the y-axis, (ii) the lower-right corner to a position 10% lower along the x-axis, and (iii) pinning down the upper-left corner. The result is shown in
Notice that we have defined a transformation which works well for objects at the depth of the door frame, but nearby objects have been distorted because the affine plane transformation cannot account for distortions at widely varying depths.
It is common for imagery to contain a number of perspective distortions. For example, the original image
shows both affine and projective type distortions due to the proximity of the camera with respect to the subject. After affine transformation, we obtain
Notice that the front face of the captain's house now has truly perpendicular angles where the vertical and horizontal members meet. However, the far background features have been distorted in the process and, furthermore, it was not possible to correct for the perspective distortion which makes the bow appear much larger than the hull,
You can interactively experiment with this operator by clicking here.
a) Experiment with different combinations of basic translation, rotation and scaling and then apply a transform which combines several of these operations. b) Rotate a translated version of the image and compare your result with the result of translating a rotated version of the image.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1986, p 321.
B. Horn Robot Vision, MIT Press, 1986, pp 314 - 315.
D. Marr Vision, Freeman, 1982, p 185.
A. Zisserman Notes on Geometric and Invariance in Vision, British Machine Vision Association and Society for Pattern Recognition, 1992, Chap. 2.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.


