Mathematical Morphology
considers digital images as discrete binary sets (lattices with a
figure-ground labeling) on which to operate.
At its basis, one adds or removes pixels from the boundaries of features in order to smooth them, to join separated portions of features or separate touching features, and to remove isolated pixel noise from the image.
Dilation turns pixels "on" according to rules based on the number or arrangement of neighboring pixels.
Erosion turns pixels "off" according to similar rules.
Opening - an erosion followed by a dilation - and Closing - the reverse sequence - attempt to restore the original area of features but with some rearrangement of the boundary pixels.
At its basis, one adds or removes pixels from the boundaries of features in order to smooth them, to join separated portions of features or separate touching features, and to remove isolated pixel noise from the image.
Dilation turns pixels "on" according to rules based on the number or arrangement of neighboring pixels.
Erosion turns pixels "off" according to similar rules.
Opening - an erosion followed by a dilation - and Closing - the reverse sequence - attempt to restore the original area of features but with some rearrangement of the boundary pixels.
Morphology for Functions
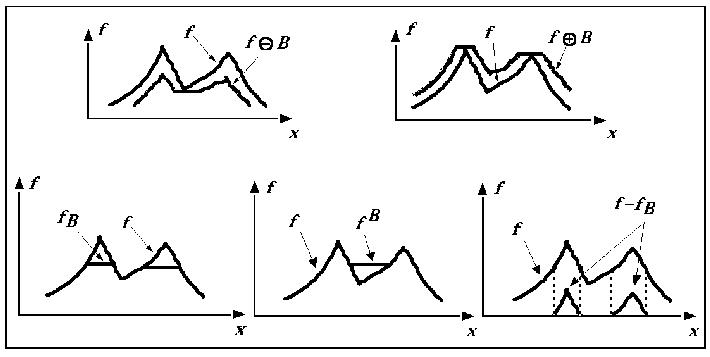
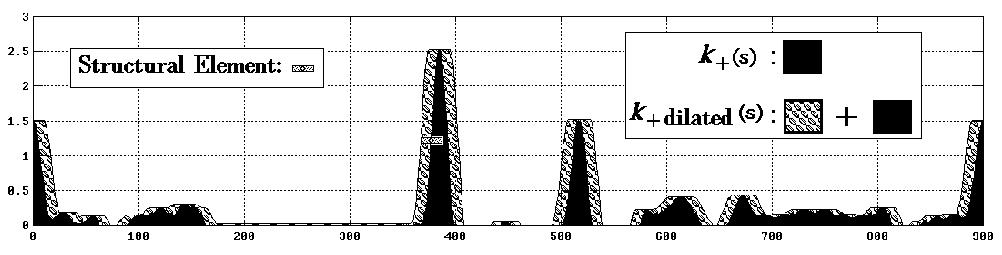
Dilation by a flat structural element.
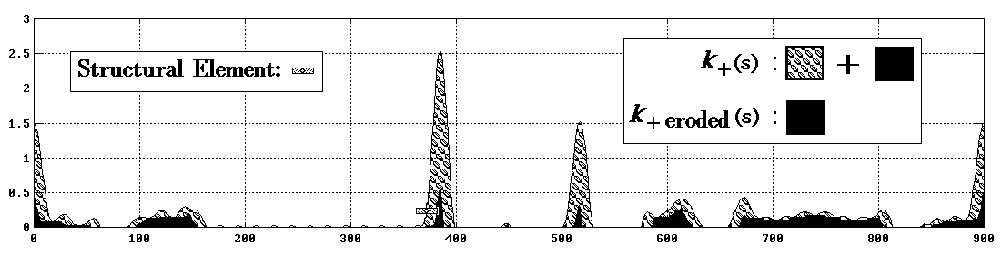
Erosion by a flat structural element.
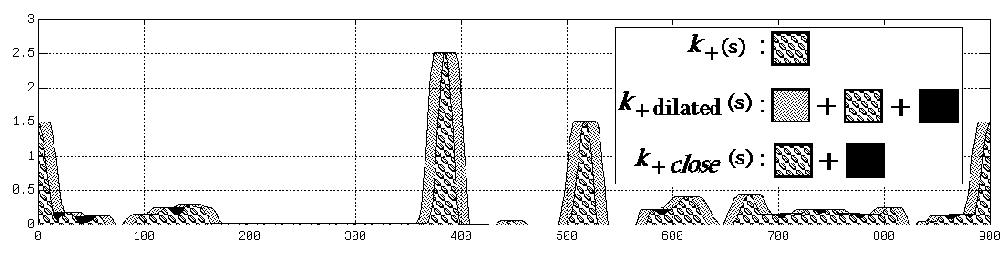
Opening : Dilation followed by Erosion: fills-in valleys (pockets)
Closing : Erosion followed by Dilation: cuts-off peaks (protrusions)
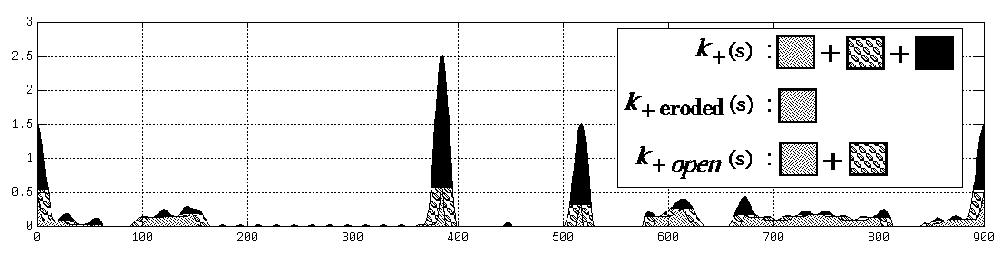
Application: Curvature morphology
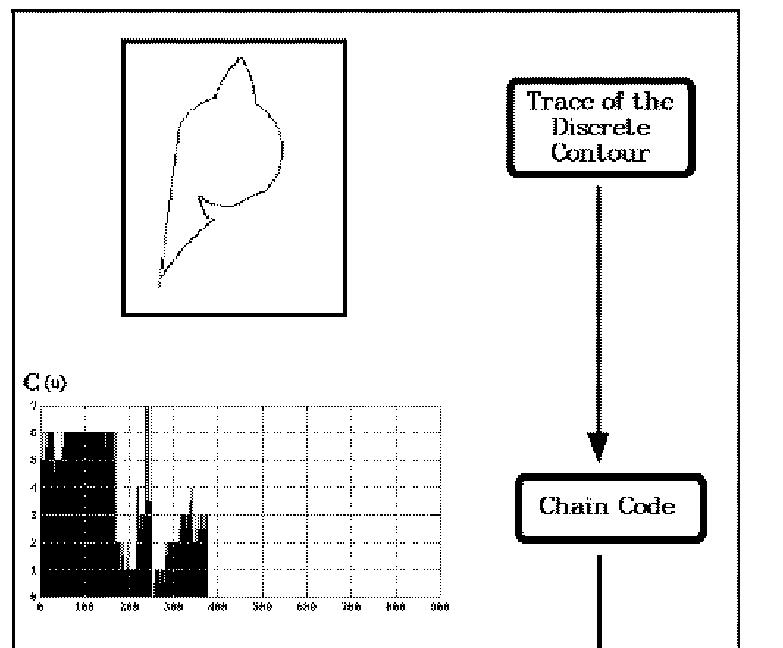
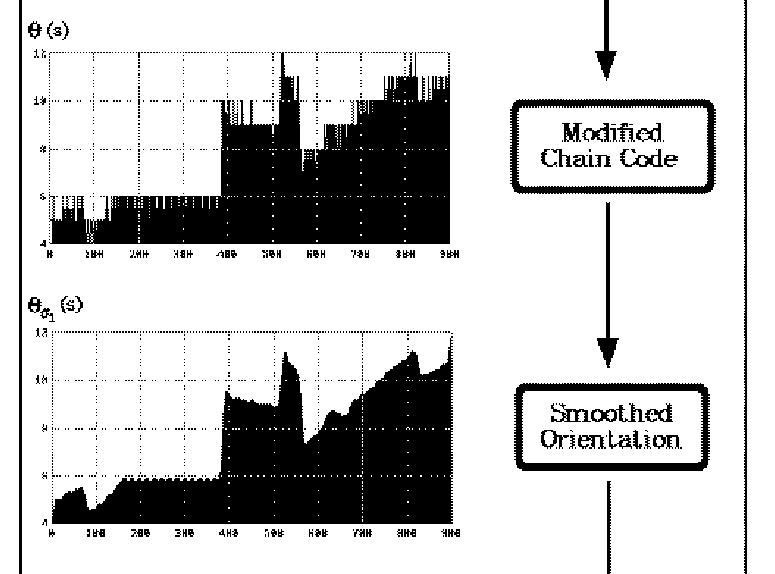
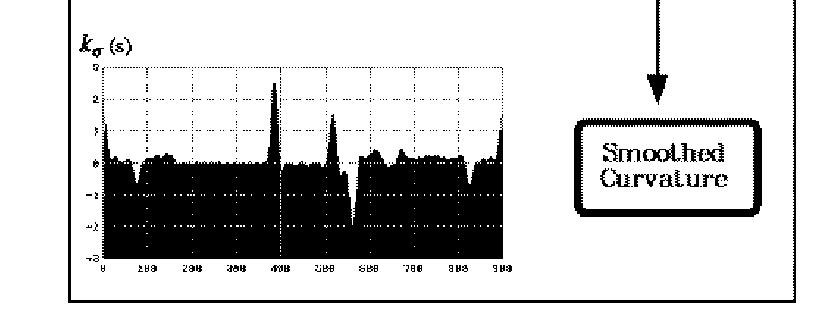
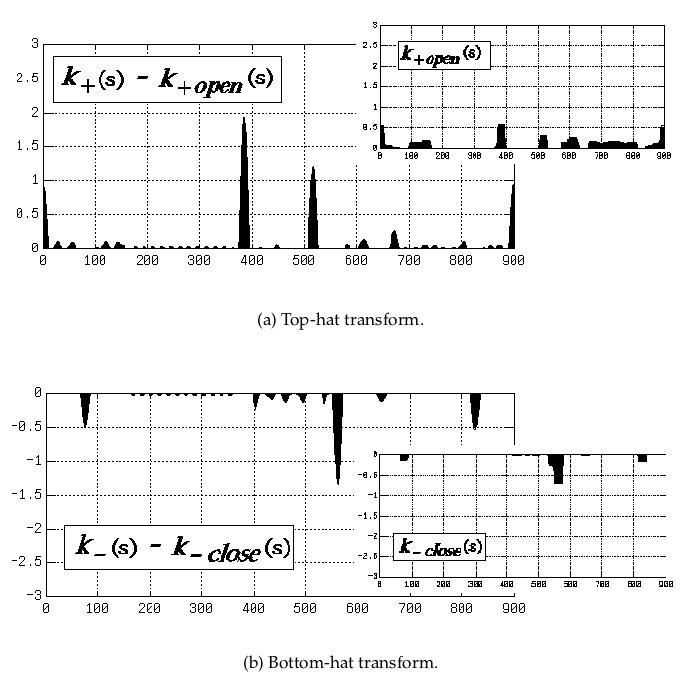
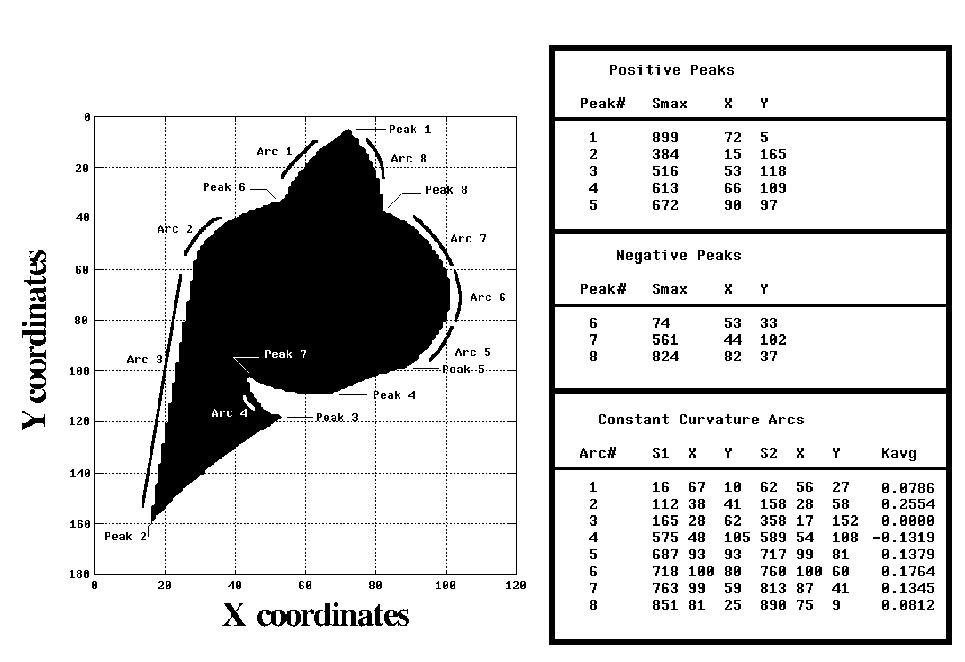
Morphology on images
(topographic surfaces)
(topographic surfaces)
Consider an image as an intensity function (of 2 variables) I(x,y).
We can apply to it the
above seqences of openings, closing, hat transforms, etc.
One particular operation is
the flooding of the topography: a dilation from minima (or sources)
conditional to the exisiting intensity values (used as mountain walls
or dams to retain the "water" --- result of dilations with flat
structural elements of non-zero height). Each source as an attached
label or color, used to distinguish flooded areas. Loci where two or
more different flooded areas meet each other create a curve of
segmentation between them (or separatrix). Such curves tend to be
along the crest lines of the intensity function seen as a topogtraphic
map (also called ridges).
The Watershed Transformation/Segmentation :
- On-line tutorial from the MMC/CMM (Beucher) : http://cmm.ensmp.fr/~beucher/wtshed.html
Morphology in 3D
-
3D Mathematical Morphology via Wave Propagation
- More Skeletons
- More 3D Skeletons