

What is noise? Noise is any undesirable signal. Noise is everywhere and thus we have to learn to live with it. Noise gets introduced into the data via any electrical system used for storage, transmission, and/or processing. In addition, nature will always plays a "noisy" trick or two with the data under observation.
When encountering an image corrupted with noise you will want to improve its appearance for a specific application. The techniques applied are application-oriented. Also, the different procedures are related to the types of noise introduced to the image. Some examples of noise are: Gaussian or White, Rayleigh, Shot or Impulse, periodic, sinusoidal or coherent, uncorrelated, and granular.
When performing median filtering, each pixel is determined by the median value of all pixels in a selected neighborhood (mask, template, window). The median value m of a population (set of pixels in a neighborhood) is that value in which half of the population has smaller values than m, and the other half has larger values than m.
This class of filter belongs to the class of edge preserving smoothing filters which are non-linear filters. These filters smooths the data while keeping the small and sharp details.
Median filtering is a simple and very effective noise removal filtering process. Its performance is particularly good for removing shot noise. Shot noise consists of strong spikelike isolated values.
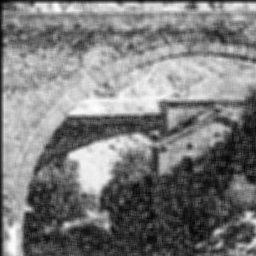
Shown below are the original image and the same image after it has been corrupted by shot noise at 10%. This means that 10% of its pixels were replaced by full white pixels. Also shown are the median filtering results using 3x3 and 5x5 windows; three (3) iterations of 3x3 median filter applied to the noisy image; and finally for comparison, the result when applying a 5x5 mean filter to the noisy image.

|

|
|---|---|
| a) | b) |

|

|
|---|---|
| a) | b) |
Comparison of the non-linear Median filter and the linear Mean filter.
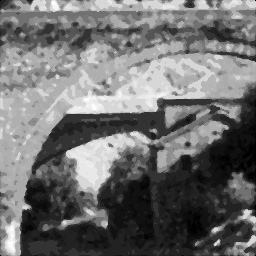
|
|
|---|---|
| a) | b) |
Observe the tradeoffs between noise reduction and the sharpness of the image when the window size is increased, and the superior performance of the median filter compared to the mean filter.