August 2, 2004
Publications in Comp. Geom. & Graphics on Voronoi Diagrams & related concepts, as well as their applications by:
BibTeX references.
Web links:
Arts & Science Professor of Computer Science at Duke University, Durham, NC 27708
Herbert Edelsbrunner
Discrete Comput. Geom., vol. 13, 415-440, 1995.
Proceedings of the ninth annual symposium on Computational geometry,
Pages: 218 - 231, San Diego, CA, 1993.
Technical report, UIUCDCS-R-93-1790, January 1993.
(University of Illinois at Urbana-Champaign Computer Science Department)
Web links:
Efficient algorithms are described for computing topological, combinatorial, and metric properties of the union of finitely many balls in R^d . These algorithms are based on a simplicial complex dual to a certain decomposition of the union of balls, and on short inclusion-exclusion formulas derived from this complex. The algorithms are most relevant in R³ where unions of finitely many balls are commonly used as models of molecules.
Keywords: power diagram.
Herbert Edelsbrunner and Ernst P. Mücke
ACM Transactions on Graphics,
Volume 13 , Issue 1 (1994), Pages 43-72.
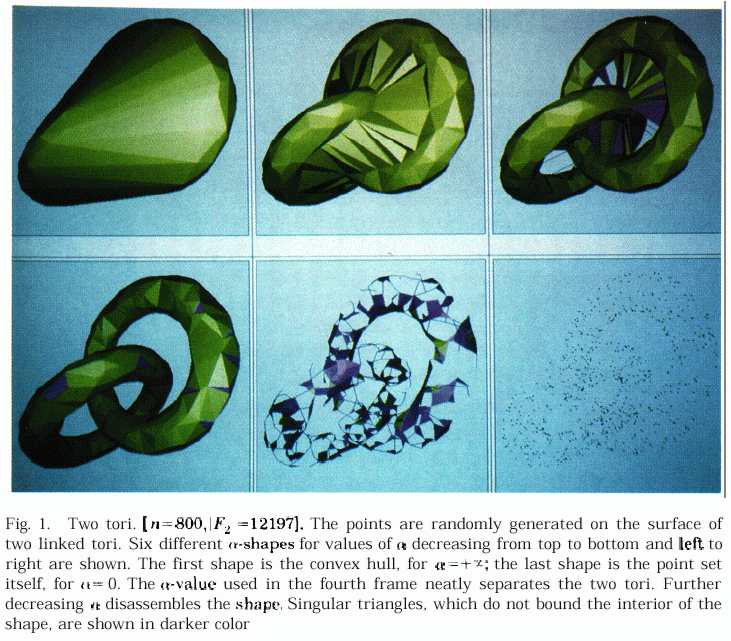
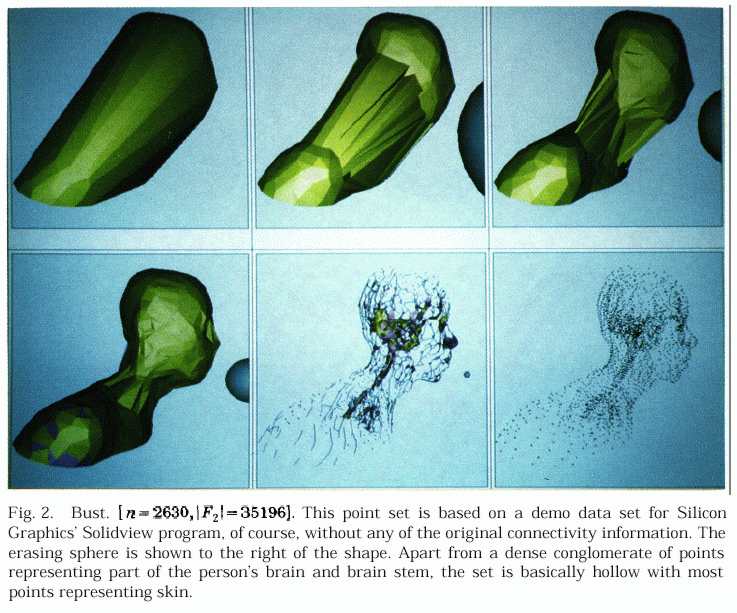
Frequently, data in scientific computing is in its abstract form a finite point set in space, and it is sometimes useful or required to compute what one might call the "shape" of the set. For that purpose, this article introduces the formal notion of the family of alpha-shapes of a finite point set in IR^3. Each shape is a well-defined polytope, derived from the Delaunay triangulation of the point set, with a parameter alpha in IR controlling the desired level of detail. An algorithm is presented that constructs the entire family of shapes for a given set of size n in time 0(n^2), worst case. A robust implementation of the algorithm is discussed, and several applications in the area of scientific computing are mentioned.
Keywords: Delaunay triangulations, computational graphics, geometric algorithms, point sets, polytopes, robust implementation, scientific computing, scientific visualization, simplicial complexes, simulated perturbation, three-dimensional space.
Goal of paper: offer a concrete and formal definition of "shape" (of point sets in IR^3).
Generalization of the concept of convex-hull:
A piece of the polytope - the generalization of polygons and polyhedra to IR^n - disappears when alpha becomes small enough so that a sphere with radius alpha, or several such spheres, can occupy its space without enclosing any of the points of the point set S - NB: similar to the empty circumsphere criterion of Delaunay.
Assumptions/Restrictions:

In chemistry and biology, alpha-diagrams are known as "space-filling diagrams": the union of all alpha-balls centered on points of S. The boundary of such diagrmas is mad of spherical caps, circular arcs and vertices. They are not restricted to equally large balls. The latter can be modeled with weighted alpha-shapes and diagrams.
The Delaunay triangulation, D, includes the union of all alpha-shapes, S_alpha, i.e., all edges and triangles of S_alpha (0 < alpha < infinity) are in D.
Sub-complexes of the "furthest-point" Delaunay triangulation of S.
A (real-valued) weight is associated to each point of S. This weight is used to set the ball radius (alpha). NB: If all points have the same weight, we are back to the Delaunay triangulation of the points.
Directly extensible, but the worst-case complexity grows exponentially (in number of faces of S_alpha).
S has at most 2n^2-5n different alpha-shapes <-- upper-bound (too pessimistic, see text).
Based on local transformations or "flips".
Geometric tests: on which side of a plane or sphere a fourth, resp. fifth, point lies. Formula for these two tests are given in terms of determinants. Similar formula are also given to comput the smallest radius of the circumsphere to an edge (2 points), a triangle or a tetrahedron.
Geometric tests for deficiding if an edge or triangle is attached or not are also given in terms of determinants.
Triangle-edge structure, interval tree or linear array.
Simulation of Simplicity (SoS) perturbs the data slightly so that all degeneracies disappear.
Automatic mesh generation and geometric modeling.
Molecular structures and protein folding analysis.
Distribution of point sets, e.g., galaxies on the universe.



Improving running time.
Maitaining Alpha Shapes.
Features and signatures:
Alvis - a 3d ALpha shape VISualizer -
[ TOP ]
H. Edelsbrunner
Notes from a lecture given in July 1993.
Compressed (gzip) postscript file: click here.
Lecture by Herbert Edelsbrunner, transcribed by Pedro Ramos and Saugata Basu. The regular triangulation has been popularized by Herbert as the appropriate generalization of the Delaunay triangulation to collections of disks. This talk was mostly devoted to definitions of Voronoi cells, nerves, simplicial complexes, Delaunay triangulations, circular inversions, stereographic projections, and their applications to computational geometry.
H. Edelsbrunner, D.G. Kirkpatrick & R. Seidel
IEEE Transactions on Information Theory, IT-29(4):551-559, 1983
Mathematical definition of Alpha shapes in 2D.
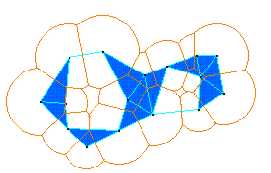
Decomposition of the union of disks and its dual complex.
Page created & maintained by Frederic Leymarie,
2000-4.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu