Feb. 11, 2004
Publications in Computational Topology by Herbert Edelsbrunner et al. :
BibTeX references.
Other related papers on Computational Geometry (link):
Other related papers on Computational Chemistry (link):
Raindrop Geomagic, Inc. : www.geomagic.com:
Company co-founder
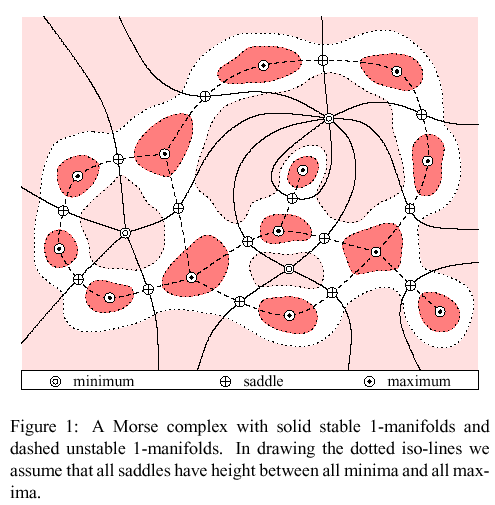
H. Edelsbrunner, J. Harer, V. Natarajan and V. Pascucci
Proc. 19th Ann. Sympos. Comput. Geom., 361-370, pp. 2003.
We define the Morse-Smale complex of a Morse function over a 3-manifold as the overlay of the descending and ascending manifolds of all critical points. In the generic case, its 3-dimensional cells are shaped like crystals and are separated by quadrangular faces. In this paper, we give a combinatorial algorithm for constructing such complexes for piecewise linear data.
Kree Cole-Mclaughlin, Herbert Edelsbrunner, John Harer, Vijay Natarajan, Valerio Pascucci
Proc. 19th Ann. Sympos. Comput. Geom., pp. 344-350, 2003.
Given a Morse function over a 2-manifold with or without boundary, the Reeb graph is obtained by contracting the connected components of the level sets to points. We prove tight upper and lower bounds on the number of loops in the Reeb graph that depend on the genus, the number of boundary components, and whether or not the 2-manifold is orientable. We also give an algorithm that constructs the Reeb graph in time O(n log(n)), where n is the number of edges in the triangulation used to represent the 2-manifold and the Morse function.
H. Edelsbrunner, J. Harer and A. Zomorodian
In Proc. of the 17th Symposium on Computational Geometry, pp.70-79, 2001.
We present algorithms for constructing a hierarchy of increasingly coarse Morse complexes that decompose a piecewise linear 2-manifold. While Morse complexes are defined only in the smooth category, we extend the construction to the piecewise linear category by ensuring structural integrity and simulating differentiability. We then simplify Morse complexes by cancelling pairs of critical points in order of increasing persistence.
Keywords: Computational topology, PL manifolds, Morse theory, topological persistence, hierarchy, algorithms, implementation, terrains

Workshop on Computational Topology, (An NSF report), Miami Beach, Florida, June 1999.
Web link: http://www.cis.ohio-state.edu/~tamaldey/computopo.html
Tamal K. Dey, Herbert Edelsbrunner, Sumanta Guha
Invited paper in Advances in Discrete and Computational Geometry, eds.
B. Chazelle, J. E. Goodman and R. Pollack. Contemporary Mathematics,
AMS, Providence, 1998(9)
Web link: http://citeseer.nj.nec.com/dey99computational.html
The authors of this article believe there is or should be a research area appropriately referred to as computational topology. Its agenda includes the identification and formalization of topological questions in computer applications and the study of algorithms for topological problems. It is hoped this article can contribute to the creation of a computational branch of topology with a unifying influence on computing and computer applications.
Keywords. Survey; topology, geometry, algorithms, computer applications.
U. Axen and H. Edelsbrunner
Mathematical Visualization, 223-236, ed. H.-C. Hege and K. Polthier,
Springer-Verlag, Berlin, Germany, 1998
Weblink: http://www.cs.duke.edu/~edels/TriTop/
Herbert Edelsbrunner and Nimish R. Shah
International Journal of Computational Geometry and Applications
Vol.7, no.4, pp.365-378, 1997.
Also appeared in the 10th Annual Symposium on Computational Geometry, 1994: 285-292.
Given a subspace X subseteq R^d and a finite set S subeseteq R^d, we introduce the Delaunay simplicial complex, D_X, restricted by X. Its simplices are spanned by subsets T \subeseteq S for which the common intersection of Voronoi cells meets X in a non-empty set. By the nerve theorem, \bigcup DX and X are homotopy equivalent if all such sets are contractible. This paper shows that \bigcup DX and X are homeomorphic if the sets can be further subdivided in a certain way so they form a regular CW complex.
Page created & maintained by Frederic Leymarie,
2001-4.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu