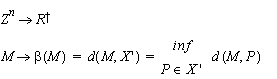
August 26, 1998
Publications by INRIA on Skeletons:
BibTeX references.
Grégoire
Malandain & Sara
Fernández-Vidal - INRIA/EPIDAURE
Image & Vision
Computing, vol.16(5), pp.317-327, April 1998.
In this paper, an algorithm to construct the approximate medial axis of a n-dimensional object is proposed. The algorithm is based on euclidean distance mapping, which guarantees the invariance under isometric transformation of the results. Skeleton points are first locally characterized, which keeps a reasonable computational cost of the method. For that purpose, we define two parameters, phi and d, whose value correspond to the detail level of the skeleton, and introduce a natural scale-space for the skeleton. Second, a threshold is chosen for one of these parameters, which gives the final detail level of the skeleton. Finally, a global step verify that the topology of the skeleton correspond to the one of the initial object.
Skeletonization should have the following properties (requirements for the global representation of objects):
Four classes of methods for skeletonization are proposed:
Let X be the object to skeletonize, a subset of Z³. The complement of X (or background) is denoted X'. The Distance Map of X, denoted ß, is defined as follows :
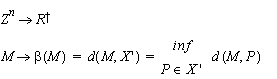
where d is the distance function. The map is computed via Danielsson's algorithm.
Then, the projection of an interior point M on the background X' is given by the following Projection Map:

The discontinuities in the Gradient of ß locate the skeletal points. A simple approximation (FDM) is first used. Then it is noted that a skeletal pixel M is such that some neighbors have very different projections on the background (i.e., there is more than one boundary point at equal distance ß). Two parameters are proposed to measure this difference in projection:
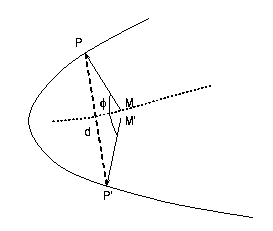
Fig.1: The 2 parameters.
These 2 parameters are related as the skeletal axis bisects the chord
angle. Thus the sinus of the bisected chord angle, phi/2, equals
the mid-chord length, d/2, divided by the projection distance to
the boundary. This definition of the chord angle is equivalent to the
bisecting angle, theta, of Meyer, used to characterize fire
propagation speed along the axis, or the alpha angle of Kruss
(twice theta): 
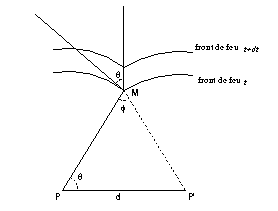
Fig.2: Relation with Meyer's bisecting angle of propagation.
How to distinguish the effect of noise on the boundary? The authors proposed to distinguish 2 types of branches:

Fig.3a: Principal branch.

Fig.3b: Secondary branch.
N.B.: These characterisations of "secondary" branches do not work with branches due to tiny holes. What is missing is a measure of "how many boundary points are creating how many skeletal points" (or vice-versa). For a tiny hole, like for a concavity of a dimple, very few boundary points create a large number of skeletal points in a continuous fashion (i.e., for some finite length axis segment or arc).
Characterisations (a) above of the 2 types of branches lead the authors to consider the depth inside the object as a relevant measure to characterise the significance of a skeletal pixel. Hence, they first propose the following bound to distinguish primary skeletal pixels/branches:
 , such that
, such that  , that is phi is between 60 and 180 degrees (from an
equilateral triangle to a completely open one).
, that is phi is between 60 and 180 degrees (from an
equilateral triangle to a completely open one).
Then the author note that f should vary as we get inside the object and become less stringent. Since f is maximally bounded to an angle of 180 deg., they consider a varying f, maximal near the background (with the condition f'(0) = 2, b below should be greater than 0.5), and propose:
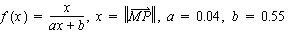
This criterion still give some breaks w/r to a correct topology; thus the authors then consider characterisations (b) above and propose the following alternative:
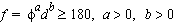
where phi is in degrees and d in number of pixels. For example, the values (a, b) = (1, 3/2) give nice results. Still homotopy is not guaranteed. Therefore, the authors have studied the topology of skeletons in 2D and 3D.
Page created & maintained by Frederic Leymarie,
1998.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu