, or in extended form : 
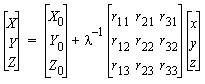. Last update, May 10, 2000
Similarity transform: rigid Euclidean transform with scaling, between the primary (X,Y,Z) and the secondary (x,y,z) coordinate systems:
, or in extended form :
.
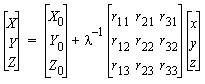The inverse transform is 
.
Seven parameters describe the transform: 
,
i.e., 3 translation steps (orthogonal), 3 rotation angles and one
scaling parameter.
This transform is called conformal, because it does not change the shape of an object (only its relative position and size).
In the image plane, non-uniform scaling in the X and Y directions as well non-orthogonal rotations, together with a translation of the origin define an affine 2D transform. More general 2D transform are expressed using polynomials of varying degrees.
The basic model is the central perspective projection (also called pin-point camera model). The primary coordinate system is positioned arbitrarily in object space, while the secondary system as its origin at the perspective camera center O, its z-axis coincides with the principal axis and is directed away from the projection (image) plane (see Fig. 2.4, p.17). The scale factor is set to unity.
In the primary system we have the coordinates of the perspective
center, O, and an object point in space, A
: 
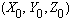and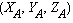 
,
respectively. The projection of A, through O,
in the image plane, expressed in the secondary system, give
the coordinates of point a :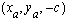 
,
where "c" is the principal distance (sometimes
called effective focal length), between O and the
principal point, PP. Points A and a
are called homologous. Thus, we have :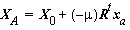 
,
where µ is a positive scalar quantity proportional to the
object distance from A to O. The reverse
tansform is then given as 
Note that the vectors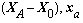 
are collinear but of opposite sense.
The 3rd equation of the reverse transform above can be written explicity in terms of the scaling µ and subsituted in the other 2 equations, leading to the Collinearity equations:
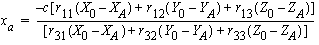and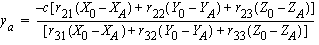 
The central perspective projection model is only an idealization (and simplification) of the actual optical geometry commonly found in cameras. Camera calibration is concerned with identifying how much the geometry of image formation differs in a real camera.
One major difference is found in the optical distortions due to lens.
Radial lens distortion causes variations in angular
magnification with angle of incidence. It is usually expressed as a
polynomial function of the radial distance from the point of symmetry
(usually coinciding with the PP):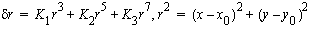 
.
Tangential lens distortion is the displacement of a point in the image caused by misalignment of the component of the lens. The displacement is usually described by 2 polynomials for displacements in x and y.
The image plane of a camera is neither completely flat, nor absolutely orthogonal to the optical axis. This is usually corrected via fiducial marks or a reseau of crosses on a glass plate fixed to camera body at the image plane. Bilinear transforms or LSE are usually used to evaluate the corrective terms.
Once the interior (calibration) parameters are known, their remains 6 exterior orientations parameters to determine (3D translation and rotation). This evaluation is called resection. At least 3 non-collinear targets such as point A above, called control points, are needed.
When more than 3 control points are available, a more rigorous statistical apporach can be used. E.g. the collinearity equations above can be linearized and a LSE used. Good initial values are required however, for the LSE process to converge to appropriate values.
Having an object point A and two homologues a1 and a2, projected in 2 images assumed calibrated and resected, the collinearity equations are used to retrieve the 3D space coordinates of A, a process called intersection (see Fig. 2.9, p.26). The problem is over-constrained, having 4 equations and 3 unknowns, and LSE can be used again. Note that thers is then onle one dof, thus results are of low reliability.
Independent resections of cameras followed by intersections of object space targets lead to small dimensional problems to resolve (6x6 and 3x3 matrices only), but are of lesser reliabilty and accuracy than the method of bundle adjustment, where large systems of equations are solved simultaneously.
Relative orientation is the evaluation of the exterior orientation elements of one camera w/r to the photo coordinate system of another camera.
Consider once again the target A with images at a1 and a2. Then the vectors :
, 
, 
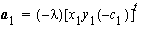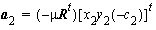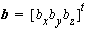
are coplanar, where b is the camera base (of the stereo pair). They lie in the epipolar plane of A and the 2 perspective centers (see Fig.2.10, p.28).
Assuming that the base vector is non-zero and using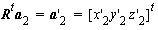 
we get the coplanarity equation for target A
:
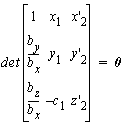
At least 3 targets are necessary (i.e., 6 constraints or coordinates)
to determine the 5 elements of relative orientation : 
.
After relative orientation has been performed, we can use the measured photo-coordinates of the 2 homologues of a target in order to evaluate, by intersection, its coordinates relative to the (x1,y1,z1) axes. Such coordinates are called model coordinates. Consider the vectors s and t, in opposite directions to a1 and a2 (i.e., pointing toward the target A). In practice, there will be no intersection of these 2 vectors in object space, because such vectors are derived from inexact photo-measurements, calibrated principal distances and estimates of exterior relative orientation elements of the camera at O2.
The parallax vector p joins s and t near the true target position: p = -µ1s + b + µ2t , where µ1 and µ2 are scalars proportional to the distance of target A to O1 and O2, respectively. The target A should lie in principle along the parallax vector. In order to specify a unique position of A on p, some constraints must be introduced. For example, in aerial mapping it is appropriate to require that the x and z component of vector p be zero. The non-zero component of p is then referred to as residual parallax or y-parallax. In close range photogrammetry one requires instead that p should have minimum length, and takes its mid-point as the position of target A.
Given the location of the homologue of A in the camera image at O1, the homologue of A in the camera image at O2 will lie along an epipolar line: the intersection of the epipolar plane, defined by the target and the 2 camera centers O1 and O2, and either of the image plane.
Any search procedure to locate a2 as a probable match to a1 can be confined to the epipolar line. In practice, however, because none of the values used to derive the equation of the line is exact, the search takes place alon a narrow band centered on the epipolar line.
DLT is a linear treatment of what is essentially a non-linear problem, so it gives only approximate values. However, DLT can be used successfully in work with non-metric cameras that do note require rigourous design and estimates of data quality, such as is the case with low cost non-metric cameras, used without fiducial marks or a réseau for image refinement,
DLT consists in first recasting the (explicit) collinearity equations into linear equations in implicit parameters. Using a sufficient number of control points (6 or more for a single image), the implicit parameters are solved via these linear equations. Finally, the explicit camera parameters can be solved in direct colsed-form from the implicit parameters.
Consider a system of n cameras disposed around an object having a typical target Ai which gives rise to an image point aij in camera j. Each target Ai is imaged in many cameras, potentially all. Then all the collinearity equations, taken together, form a set of equations which is called functional model of the photogrammetry system : F(x, b, a) = 0 , where x is a vector representing the u elements whose values are required (i.e., the parameters to be estimated), b is vector representing the m measured elements and a is a vector representing elements whose values are known constants; thus, we aim at evaluating x given b and a. Generally no unique solution exists for x, but least square estimation (LSE) provides means for obtaining a useful one.
If cameras have been calibrated a priori, the calibrated values may be included in a and ketp fixed, or included in b and x to be re-evaluated. If no prior calibration is available, the calibration elements can be included in x only, a procedure known as self-calibration.
Page created & maintained by Frederic Leymarie,
1998-2000.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu