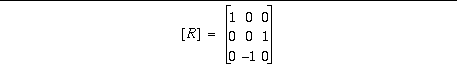
Dimensional
Analysis through Perspective,
by James R. Williamson & Michael H. Brill
ASPRS, 1990
| Back | Next |
What is known a-priori in this case:
This is the most coomon case found in paintings or photographs, where the image x-axis is parallel to the ground level of horizon. Then the camera has no "roll".
The camera is allowed to roll around its optical axis w/r to the horizon or ground plane; then:
Constant rotation matrix:
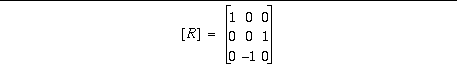
Only one varying angle, the swing s :
r11 = - cos(s) r12 = 0 r13 = -sin(s)
r21 = sin(s) r22 = 0 r23 = -cos(s)
r31 = 0 r32 = -1 r33 = 0
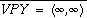 and
and 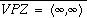 .
.
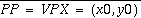 .
.
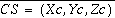
We assume no fiducials are available; otherwise the PP is trivial to retrieve (intersection of the 2 perpendiculars defined by the 4 fiducials, usually at the center of the image canvas). We also assume that the image canvas was possibly "cropped" (or painted so that the PP is not at the center of the canvas); thus we cannot use intersection of diagonals from the 4 canvas corners.
Therefore, we are left with only one choice: drawing the VPX as the convergence of parallels. So here, we are back to the old Leonardo's method from Renaissance. Note that this is the underlying method for TIP (although it was not formally used which leads to inaccuracies in obtaining a grid or web).
Locate the VPX where parallel lines in depth (receding from you) converge. This should be a point somewhere near the center of the canvas in general (but not always!).
Try to pick lines in the scene which are not too close to each other (so that the intersection angle is greater) and which have a longer support in the image (a longer segment trace which you have to extend usually to find the VP). The VP may not be at the center of the canvas or can even be outside the canvas. This can be expected if your eye is "driven" in a direction other than towards the center of the canvas (a "trick" used by photographs of painters).
Thus, from a number of converging lines we get an approximation of the PP as their intersection:
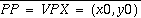 .
.
If the lines all intersect at one single point, the accuracy is excellent. Otherwise, a best fit must be found for this intersection, analytically or by having the user move around a small circle whose center will be the best (visually speaking) intersection point.
From this point we can draw the True Horizon Line (THL): it is a line going through PP and parallel to the horizontal direction of the image frame or canvas (i.e., parallel to the x axis).
Draw the PP as the intersection of converging parallels, receding in depth from the user view point.
Draw the THL as an horizontal through the PP.
Given known diagonals in the image of 45 degrees, two additional VP's can be defined to the left and right of the PP, along the THL; we call them VPXL and VPXR. The (average) distance from each of these 45 degree VP's to the PP is the effective focal length. If the 2 distances are not equal, take the average as a better approximation (this is the sign of an inaccurate VP positioning).
Such VPs can be found if there exist a known "square" in the scene which is projected as a perspective rectangle in the image canvas. This square must have one of its major axis converging to the PP. The more squares the better, e.g. a checkerboard floor or ceiling is useful here. Note that the "square" can alternatively be a squared diamond, an hexagon, ..., or even a circle! (or any regular "polygon" oriented towards the PP, the circle being the "limiting" object).
Alternatively, if no such "square" is to be found, an object which appears both in an object-space plane (parallel to the image plane here) and in a plane receding in depth and going through the PP, can be used to derive a perspective rectangle (square in object space) from which the 2 VP can be found. E.g. in an interior scene, a door (window) can appear in both planes, the width of which can be used to draw the needed square.
Assuming we have found VPXL and VPXR, the effective focal length is then:
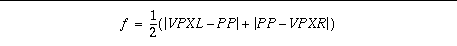
In the case of a painting, this is the distance from the eye (retina) of the painter to the canvas at the locus of PP.
We first need to establish a scale, S, and the object-space coordinate system [O , X , Y , Z]. To do so, we will need the user to identify a "dimension" (of an "known" object) parallel to one of these major axis planes. But first, the user needs to specify a position for the origin of the object-space coordinate frame, O, as well as the orientation of the 3 main axes. In practice, it is convenient to select a "corner" in the scene on what looks like the ground or floor level (or eventually the ceiling).
We assume the object-space origin in not placed at PP. Otherwise the CS coordinates are trivial: (0 , f'/S , 0), and we need a scale along the horizon line, which might not be available. Furthermore, the "ground plane" is then through the THL and the eye , thus we cannot distinguish it from this horizon ... For more flexibility, we assume in the remaining, that O is not at PP.
From the dimension (scale), we can compute a first CS coordinate. Then, we can always compute the remaining two camera coordinates. Note that, if the user does not know true dimensions of any object in the scene a SWAG (Scientific Wild Alternate Guess) is always a good start! "The world can only be grasp by action, not by contemplation . . . " (J.Bronowski). At worse, our measurements we will be off by some scale factor.
N.B.: An alternative to performing SWAGs is available if we have a map (or blueprint) of the scene. Then it is easy to find 2 of the coordinates of CS (the ones along the ground plane axes if these are taken to be parallel to the 2D map axes). This is a variation (simplification) of Chasles Theorem.
The user selects a reference frame position:
The user identifies the dimension of some "known" object (segment length) in the scene, parallel to either the X-Y, X-Z or Y-Z (object-space) planes:
Additional input:
Additional input:
There are 3 sub-cases, whether the identified dimension D is parallel to X-Y, X-Z or Y-Z planes. But first, common computations are required:
| Back | Top | Next |