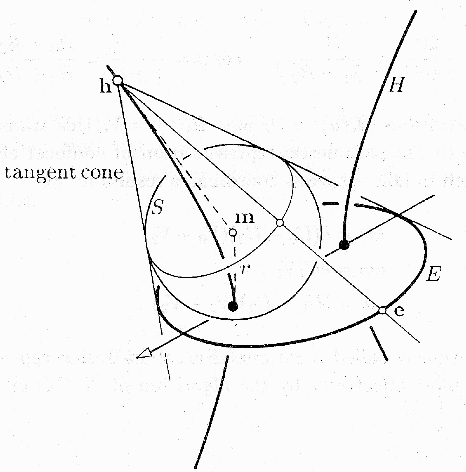
From [Boehm94], p. 196 .
Last update, Dec. 17, 2001
The vertices h of all real right cones (i.e., which circumscribes a sphere) which contain a given ellipse
E : x²/a² + y²/b² = 1 , z = 0 , a > b
lie on the hyperbola
H : x²/e² - z²/b² = 1 , y = 0 , e² = a² - b²

From [Boehm94], p. 196 .
H (E) lies in a plane perpendicular to E (H), along the main axis of E (H) and goes through the foci of E (H). That is, the foci of E and H are the vertices of H and E, respectively.
Every cone circumscribing a quadric of the family
Q : x² / (a² - µ) + y² / (b² - µ) +
z²/(-µ) = 1
µ < 0 , then Q is an ellipsoid
0 < µ < b² , then Q is an hyperboloïd of 1 sheet
b² < µ < a² , then Q
is an hyperboloïd of 2
sheets
is a right cone if its vertex is on E or H.
E and H are then called the focal conics of Q and this family of quadrics is called confocal.
Pair of parabolas which lie in perpendicular planes, and such that the focus of each parabola is the vertex of the other one. One focus of each parabola is considered to be at infinity (w/r to the ellipse-hyperbola case).
Then, the vertices of right cones which are circumscribed about a paraboloid lie on such focal parabolas.
Focal conics are also called "linked conics": A pair of plane conics that lie in perpendicular plane and such that each passes trough the foci of the other. One conic is the linked conic of the other, and vice-versa. Besides the ellipse-hyperbola and parabola-parabola pairs, the following degenerate cases are also possible:
Generalized string construction of E with respect to H:
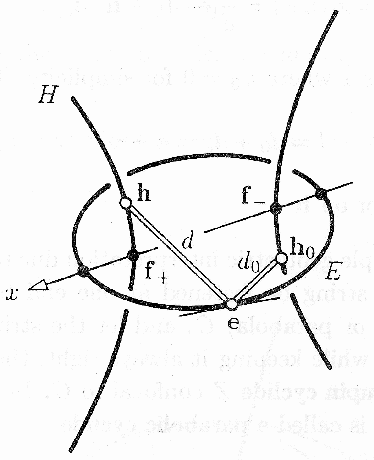
From [Boehm94], p. 199 .
Page created & maintained by Frederic Leymarie,
1998-2001.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu