Last update, Dec. 17, 2001
BACK
Geometric concepts for Surfaces in 3D
Envelope of any one parametric family of spheres. It traces out a
tubular surface swept out by the spheres, with varying radius, moving
along a space curve, the axial curve.
Properties :
-
Any such sphere of this family is in contact with the
surface along a circle. Such circles form a one
parameter family of curvature lines of the surface.
-
The offset of a canal surface is a canal surface.
Examples :
-
All surfaces of revolution,
where the axis is a straight line segment.
-
Dupin's cyclides.
References :
Definition:
In principal axes coordinates, confocal cones are defined by
C : x² / (a² - µ) + y² / (b² - µ) +
z²/(-µ) = 0
Properties :
-
Tangent cones from any point in 3D space to a family of
confocal quadrics form a family of confocal cones.
-
A family of confocal cones C contains one pair of
real focal rays and 2 imaginary pairs.
-
A family of confocal cones C intersects a
concentric sphere in a family of so-called spherical conic
sections.
Definition :
A quadric of the family
Q : x² / (a² - µ) + y² / (b² - µ) +
z²/(-µ) = 1
µ < 0 , then Q is an ellipsoid
0 < µ < b² , then Q is an hyperboloïd of 1 sheet
b² < µ < a² , then Q
is an hyperboloïd of 2
sheets
uniquely determined by its focal
conics E and H .
From [Boehm94], p. 197
Properties :
Theorem [Hilbert32 , p.24]:
-
Every surface of the confocal system, when viewed
from a point lying on a focal conic, and not enclosed by the given
surface, looks like a circle with its center on the
line of sight (optical axis), provided the line of sight is tangent to
the focal curve.
Elliptic coordinates :
These confocal quadrics intersect each other in space at right angles
and fill-up space, thus determining elliptic coordinates for 3D space;
together they form what we call a confocal system. Thus
for any point is 3D space, [ x y z ] there are 3
(orthogonal) members of the family containing this point.
Jacobi's Theorem [Arnold89 , p.471]:
-
Through each point of an nD Euclidean space there pass n
quadrics confocal to a given ellipsoid. Smooth confocal quadrics
intersect at right angles.
Chasles' Theorem [Arnold89 , p.471]:
-
Given a family of confocal quadrics in nD Euclidean space, a line
in general position is tangent to n - 1
different quadrics in the family, and the planes tangent to the
quadrics at the points of tangency are pairwise orthogonal.
Chasles' Lemma [Arnold89 , p.472]:
-
The apparent contours of the quadrics (i.e., the set
of critical values of the projection of a quadric) in a confocal family
form themselves a confocal family of quadrics.
Theorem on geodesics and tangency [Arnold89 ,
p.472]:
-
Given a geodesic on a quadric Q in nD
Euclidean space, there is a set of n - 2 quadrics
confocal to Q such that all the tangent lines to the
geodesic are also tangent to the quadrics in the set.
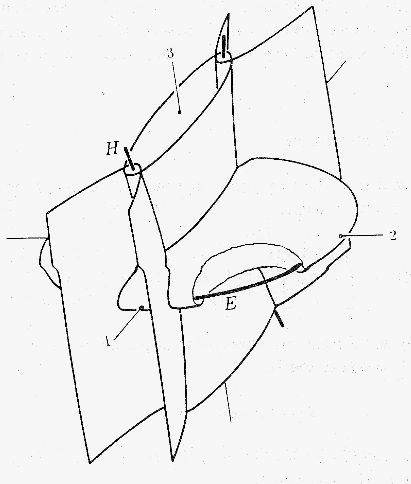
Degenerate conics :
-
The focal conics E and H can be
considered as degenerate (flat) members of the family of quadrics Q,
where µ = 0 and µ = -b²,
respectively.
-
E and H meet each quadric of the
confocal family in its umbilical points.
-
A confocal family of quadrics also contains 2 imaginary focal conics,
one in the plane x = 0, for µ = -a²,
and one in the ideal plane
("at infinity") for µ = æ,
called the absolute spherical circle.
Reflective property :
-
Light emanating from the focal ellipse E in direction
of a focal ray (i.e., towards H) is reflected by a
confocal ellipsoid Q in the direction of a focal ray
back to E.
Applications :
-
Study of motion with fixed pull in a field with one
attracting center - geodesics on a triaxial ellipsoid
[Arnold89, pp.261-266].
-
Magnetic analogues to Newton's (Ivory's) theorem on the gravitational
attraction of a sphere (ellipsoid) [Arnold89, pp.475-479].
References :
Surface obtained as the envelope of 2 one-parameter families of spheres
moving along a pair of focal conics. This surface is said
to be confocal to the pair of (focal) conics.
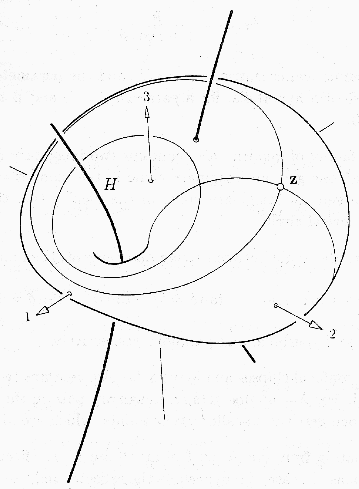
Dupin's cyclides are a special group within the family of cyclides.
Definitions :
Several equivalent definitions are possible; 3 are given below [Hirst90]
:
-
The enveloppe of a family of spheres having their centres
on one (focal) conic and all passing through a point
on its linked (focal) conic. N.B.: The latter point
may be imaginary, but still satisfy the linked conic's equation.
-
A surface in R³, possibly with singularities, all of
whose lines of curvature are "circles"
(including the limiting cases of a straight line and point).
-
A surface in R³, possibly with singularities, whose focal
set (i.e., loci of centres of curvature) is a finite union of smooth
connected manifolds of dimension less than 2. N.B.: the
manifolds are focal conics.
For more on alternative definitions, see (in French):
Geometric construction:
Due to Maxwell (1868); based on the use of focal rays;
see [Boehm94, p.200].
Let a sufficiently long string be fastened at one end to the focus of a
focal conic, C, and let the string slide smoothly over
this conic section while keeping it always tight; then the unfastened
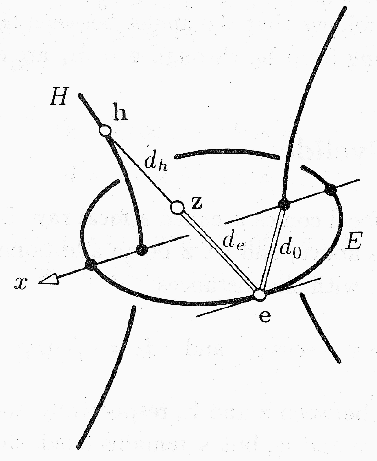
end will sweep out a Dupin cyclide Z confocal to C.
From [Boehm94], p. 201
Properties :
-
Dupin's cyclide is a canal surface.
-
They are the only surfaces where
both families of (principal) curvature lines are circles.
-
The cyclide is enveloped by a 1st family of spheres
around the points e of E with radii de
and a 2nd family of spheres around points h
of H with radii dh .
-
Confocal Dupin's cyclides are offsets
of each other.
-
A system of confocal cyclides can be regarded as a system of wave
surfaces in an isotropic medium
corresponding to the focal rays from a fixed point on one focal conic
reflected by the other focal conic [Boehm94 , p.203].
-
A cyclide is a real algebraic surface of order 4 in the
general case. In the special cases of a sphere or a cylinder, it is of
lower orders.
Classification (after Maxwell) [Hirst90]
:
-
Elliptic or Hyperbolic Cyclides: the
linked conics are the ellipse (E) and hyperbola (H).
-
Spindle Cyclide:
The fixed point on H is real and the one on E is imaginary.
-
Horned Cyclide:
The fixed point on H is imaginary and the one on E is real.
-
Ring Cyclide: The 2 fixed
points are imaginary.
-
Symmetric Cyclides: The focal ellipse and hyperbola
have degenerated into a circle and a straight line.
-
Symmetric Spindle Cyclide
-
Symmetric Ring Cyclide: a torus.
-
Parabolic Cyclides: The linked conics are 2
parabolas.
-
Parabolic Horned Cyclide: one fixed point is imaginary
and the other is real; with limiting case the Parabolic Crescent
Cyclide.
-
Parabolic Ring Cyclide: Both fixed point are imaginary.
-
Cylinders and Cones: The focal set if a
single straight line, the other conic lying at infinity. One
family of lines of curvature consists only of straight lines and the
corresponding family of generating spheres consists of planes. If these
planes (or straight lines of curvature) all pass through a real fixed
point, then we have a cone. Otherwise, if they pass through
an imaginary fixed point (at infinity), we have a cylinder.
-
Spheres: The focal set consists of a single real
point.
-
Planes: The focal set consists of a single imaginary
point (taken to infinity).
Examples :
-
If one of the focal conic is a circle (the other one
becomes a straight line, along the normal to the circle's plane,
through its center), then the cyclide is a torus.
Applications :
-
For blending surfaces in Computer Aided Design:
in particular blending (joining) cones/cylinders and planes [Hirst90].
References :
Definition:
Conics in the tangent plane which, together with
Meusnier's sphere, completely describes the curvature
properties at a point of a surface. The indicatrix is defined as a
pair of conics obtained by expanding
an equation in Monge's Form z=F(x,y) in a Maclaurin Series.
Geometric construction:
Translate the tangent plane along the normal at a point p
of the surface. The intersection curve, at a fixed distance (an
infinitesimally small amount d) from the normal axis,
describes the conics. This curve is projected orthogonally onto the
tangent plane and scaled by 1/sqrt(2d) .

From [Boehm94] , p. 288
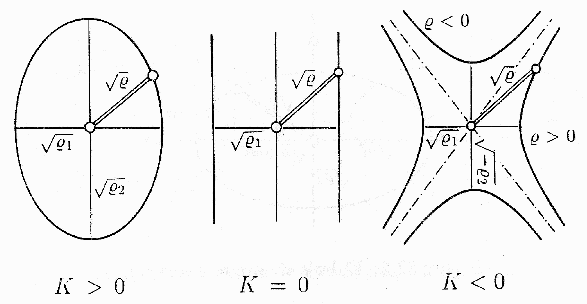
For a smooth surface, this will be an ellipse, parabola, hyperbola,
parallel straight lines, circle or point.
From [Boehm94] , p. 377
Properties :
-
At umbilical points, the indicatrix is a circle.
-
The radius of the indicatrix in any direction is equal to the Square
Root of the Radius of Curvature in that direction.
-
The size of the (constructed) indicatrix depends on the scale
used [Boehm94, p.288].
References :
-
[Boehm94], pp. 376-379
-
Coxeter, H. S. M. ``Dupin's Indicatrix'' §19.8 in Introduction to
Geometry, 2nd ed. New York: Wiley, pp. 363-365, 1969.
Page created & maintained by Frederic Leymarie,
1998-2001.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu