Next: References
![]()
![]()
![]()
Next: References
F. Leymarie
January 2000 - updated September 2003
Update (Sept. 2003):
The number K(x_1 , x_2 , x_3) = 1/ R , where R is the radius of the circumcircle through the three points x_1 , x_2 , x_3 , is called the Menger curvature of the triple [3].
The derivation of the formula below, then relies on using the well known relation between the area of the triangle, A, through these three points and R:
K=1/R = 4 A / abc , where a, b and c are the length of the sides of the triangle.
Note that Heron's formula gives us:
16 A^2 = (a+b+c) (b+c-a) (a+c-b) (a+b-c)
and this directly give the formula below. An alternative formula is provided by the Cayley-Menger determinant [1], which avoids directly computing the side lengths (as square roots): 16A^2=| a^2(a^2-b^2-c^2)+b^2(b^2-a^2-c^2)+c^2(c^2-a^2-b^2)|.
Let f be a regular curve of class C2 in a Euclidean space, En. Let x1,x2,x3 be distinct points of f. Then, define [1, vol.1, p.273]:
![]()
where the (non-negative) number K is called Menger's curvature. As x2 and x3 approach x1 on f, K(x1,x2,x3) tends towards the curvature of f at x1. Also, K=0 if and only if x1, x2 and x3 are collinear .
In the complex domain, for ![]() ,
this notion is called the Menger-Melnikov curvature [2]:
,
this notion is called the Menger-Melnikov curvature [2]:
![]()
where the sum is taken over all permutations of ![]() of
of ![]() .This
identity is transformed for 1-sets in En to:
.This
identity is transformed for 1-sets in En to:
![]()
or equivalently, after some manipulations:
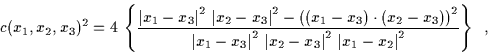
which, by Schwartz inequality, can be shown to always be non-negative.