
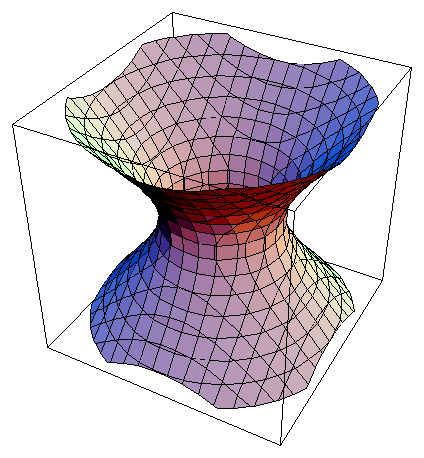
Hyperboloid of One Sheet; where a = 2.5 .
July 11, 2000
Publications on Representations in Object Modeling:
BibTeX references.
Vinod Kumar, D.
Burns, Debasish
Dutta and Christof
M. Hoffmann
Computer-aided
Design, Vol. 31 (9), pp. 541-556, August 1999.
Modeling of products (objects) form a critical task in design and manufacturing. CAD-CAM techniques based on solid/geometric modeling have been developed for this purpose. Primarily, these methods capture the shape of the object. However, recent developments in diverse fields demand modeling schemes, which extend beyond the shape to include other relevant attributes of the object. In this paper, this issue is addressed and a new modeling framework is proposed. This framework enables the modeling of geometry and several attributes simultaneously in an integrated fashion.
Keyword(s): Solid modeling; CAD-CAM techniques; Geometry and attribute representation.
Uses the fiber bundle formalism of differential geometry.
John K.
Johnstone and C.-K. Shene
Technical Report 91/19, Department of Computer Science
Johns Hopkins University, Baltimore, Maryland, USA, 1991.
We show that all hyperboloids of one sheet and hyperbolic paraboloids can be represented by two lines. This representation makes it easier to use the hyperboloid of one sheet as a fundamental primitive like the sphere, including input, display and computations (such as rigid transformation and point classification). The new representation also provides insight to the bisector.
The simple bisector or weighted bisector of two lines only represents small subclasses of the hyperbolic paraboloid and hyperboloid of one sheet. We extend to the bisector and weighted bisector of two skew lines with respect to a plane, and show that they exactly represent the hyperboloid of one sheet and the hyperbolic paraboloid. Since our results are constructive, they yield formulae for the two lines that represent a given surface.
Keywords: representation of surfaces, design, quadric surfaces, bisector, solid modeling.
Algebraic definition (in normal form) of the hyperboloid of one sheet:
x²/a² + y²/b² - z²/c² = 1 , a >= b
or
(x, y, z) = (a cosT coshP, b sinT sinhP, c sinhP) , 0 <= T <= 2pi , -pi <= P <= pi

Hyperboloid of One Sheet; where a = 2.5 .
When a = b = c = 1, one gets the simpler formula :
x² + y² - z² = 1
Closely related is the hyperbolic paraboloid :
x²/a² - y²/b² = c z

Hyperbolic paraboloid, where a = 1 , b = 2 & c = 3
.
It is difficult to extract the geometry of a surface given such algebra: given a polynomial, what surface does it represent? Given a surface, what polynomial represents it?
It proves useful to develop a representation based directly on the geometry of the surface, similar to the representation of a sphere by its center & radius. Geometric representations are excellent for design and input and are more robust under rigid transformations.
Representation of a surface by its distance from a collection of geometric objects (e.g. a cylinder as the equidistant locus from a line). One can represent a complicated object in terms of a small number of simple objects of lower degree and dimension. Intersection algorithms can be derived. Bisectors in E² or E³ can be computed.
N.B.: When alpha = 1, the alpha-bisector reduces to the bisector definition.
When alpha = 1, the conic is the parabola; for alpha < 1 it is the ellipse, and for alpha > 1 the hyperbola.
 |
 |
 |
alpha = 1 : parabola |
alpha < 1 : ellipse |
alpha > 1 : hyperbola |
E.g., the distance representation of a parabola is {O = {P, L}, s.t. f:= dist(x, P) = dist(x, L)}, where P is a point not on the line L.
x²/a² + (1/a² + 1/c²) y² - z²/c² = 1 , a >= b
(x² - y²)/a² = z
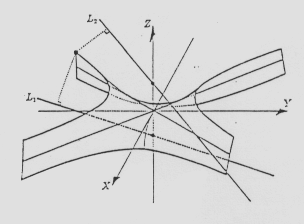
The bisector of two skew lines is a right hyperbolic
paraboloid.
{(x2-x1)² + (y2-y1)² + (z2-z1)² }- {µx (x2-x1) + µy (y2-y1) + µz (z2-z1) }
N.B.: This distance formula is the square root of a polynomial of degree 2, and the sum or difference of distances from two skew lines will be a degree 4 expression.
L1k : [ 0, 0, a² k / 2(1+k²) ] + t [1-k, 1+k, 0]
L2k : [ 0, 0, -a² k / 2(1+k²) ] + t [1+k, 1-k, 0]
where k is any non-zero real number.
E.g., consider the lines L1: (0, 0, l) + t (1, k, 0) and L2: (0, 0, -l) + t (1, -k, 0). Consider the squared distance from any point (x, y, z) to L1 and L2 by d1² and d2², respectively. The set of equidistant points, s.t. d1² = d2² is then given by:
-k (x·y) / l(1+k²) = z
or, through a clockwise rotation of 45°:
k (x²-y²) / 2l(1+k²) = z
Then, let l = a² k / 2(1+k²) to get the desired surface as the bisector.
Page created & maintained by Frederic Leymarie,
1998-2000.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu