Last update: July 31, 2004

BACK

References in Computational Geometry and Graphics: Level Set Methods for Shape

• Jim Blinn:
  • A Generalization of Algebraic Surface Drawing, 1982.
• J. C. Carr et al. :
  • Smooth surface reconstruction from noisy range data, 2003.
  • Reconstruction and Representation of 3D Objects with Radial Basis Functions, 2001.
  • Surface Interpolation with Radial Basis Functions for Medical Imaging, 1997.
• H. Hoppe et al. :
  • Surface Reconstruction from Unorganized Points, 1992.
• N. Kojekine et al. :
  • Surface reconstruction based on compactly supported radial basis functions, 2004.
  • Software Tools Using CSRBFs for Processing Scattered Data, 2003.
• M. Levoy et al.:
  • A Volumetric Method for Building Complex Models from Range Images, 1996.
• C. T. Lim et al. :
  • Implicit Reconstruction of Solids from Cloud Point Sets, 1995.
• W. Lorensen et al.:
  • Marching Cubes: A High Resolution 3D Surface Construction Algorithm, 1987.
• B. S. Morse et al. :
  • Interpolating Implicit Surfaces from Scattered Surface Data Using Compactly Supported Radial Basis Functions, 2001.
• S. Muraki :
  • Volumetric Shape Description of Range Data using "Blobby Model", 1991.
• T. Poston et al.:
  • Multiresolution Isosurface Extraction with Adaptive Skeleton Climbing, 1998.
• H.-P. Seidel, A. Belyaev, G. Turk et al. :
  • Multi-level Partition of Unity Implicits, 2003.
  • Modelling with Implicit Surfaces that Interpolate, 2002.
• H.-K. Zhao, S. Osher et al.:
  • Visualization, Analysis and Shape Reconstruction of Unorganized Data Sets, 2002.
  • Fast Surface Reconstruction Using the Level Set Method, 2001.

BibTeX references

(Introduces Blobby Modelling.)

Web link:

• ACM portal

Web links:

• http://aranz.com/research/modelling/theory/
• ACM portal: http://doi.acm.org/10.1145/604471.604495

This paper shows that scattered range data can be smoothed at low cost by fitting a Radial Basis Function (RBF) to the data and convolving with a smoothing kernel (low pass filtering). The RBF exactly describes the range data and interpolates across holes and gaps. The data is smoothed during evaluation of the RBF by simply changing the basic function. The amount of smoothing can be varied as required without having to fit a new RBF to the data. The key feature of our approach is that it avoids resampling the RBF on a fine grid or performing a numerical convolution. Furthermore, the computation required is independent of the extent of the smoothing kernel, i.e., the amount of smoothing. We show that particular smoothing kernels result in the applicability of fast numerical methods. We also discuss an alternative approach in which a discrete approximation to the smoothing kernel achieves similar results by adding new centres to the original RBF during evaluation. This approach allows arbitrary filter kernels, including anisotropic and spatially varying filters, to be applied while also using established fast evaluation methods. We illustrate both techniques with LIDAR laser scan data and noisy synthetic data.

Web links:

• http://aranz.com/research/modelling/theory/

We use polyharmonic Radial Basis Functions (RBFs) to reconstruct smooth, manifold surfaces from point-cloud data and to repair incomplete meshes. An object's surface is defined implicitly as the zero set of an RBF fitted to the given surface data. Fast methods for fitting and evaluating RBFs allow us to model large data sets, consisting of millions of surface points, by a single RBF - previously an impossible task. A greedy algorithm in the fitting process reduces the number of RBF centres required to represent a surface and results in significant compression and further computational advantages. The energy-minimisation characterisation of polyharmonic splines result in a "smoothest" interpolant. This scale-independent characterisation is well-suited to reconstructing surfaces from non-uniformly sampled data. Holes are smoothly filled and surfaces smoothly extrapolated. We use a non-interpolating approximation when the data is noisy. The functional representation is in effect a solid model, which means that gradients and surface normals can be determined analytically. This helps generate uniform meshes and we show that the RBF representation has advantages for mesh simplification and re-meshing applications. Results are presented for real-world rangefinder data.

Web links:

• http://aranz.com/research/modelling/theory/

Radial basis functions are presented as a practical solution to the problem of interpolating incomplete surfaces derived from three-dimensional (3D) medical graphics. The specific application considered is the design of cranial implants for the repair of defects, usually holes, in the skull.

Radial basis functions impose few restrictions on the geometry of the interpolation centers and are suited to problems where the interpolation centers do not form a regular grid. However, their high computational requirements have previously limited their use to problems where the number of interpolation centers is small (<300). Recently developed fast evaluation techniques have overcome these limitations and made radial basis interpolation a practical approach for larger data sets.

In this paper radial basis functions are fitted to depth-maps of the skull's surface, obtained from X-ray CT data using ray-tracing techniques. They are used to smoothly interpolate the surface of the skull across defect regions. The resulting mathematical description of the skull's surface can be evaluated at any desired resolution to be rendered on a graphics workstation, or to generate instructions for operating a CNC mill.

Web link:

• http://grail.cs.washington.edu/pub/abstracts.html
• http://research.microsoft.com/~hoppe/

We describe and demonstrate an algorithm that takes as input an unorganized set of points {x1,...,xn} in R^3 on or near an unknown manifold M, and produces as output a simplicial surface that approximates M. Neither the topology, the presence of boundaries, nor the geometry of M are assumed to be known in advance - all are inferred automatically from the data. This problem naturally arises in a variety of practical situations such as range scanning an object from multiple view points, recovery of biological shapes from two-dimensional slices, and interactive surface sketching.

Summary of the algorithm:

1. Build the Euclidean Minimum Spanning Tree (EMST) for the unorganized points (O(n²) complexity).
    
2. Riemannian graph: add new edges to the EMST, by considering the k-nearest neighbors to each sample (O(n+k log(n)) complexity).
    
3. Build consistently oriented tangent planes by propagation along the Riemannian graph.
    
4. Estimate the signed distance function from the oriented tangent planes at a discrete set of grid (voxel) loci.
    
5. Produce a first approximation of the surface via a modified marching cube algorithm.
    
6. Post-processing to remove triangles with a poor aspect ratio using edge-collapse (preserves the topology):
   • Build a priority queue of edges using the edge length times the minimum inscribed radius of its two adjacent triangular faces.
      

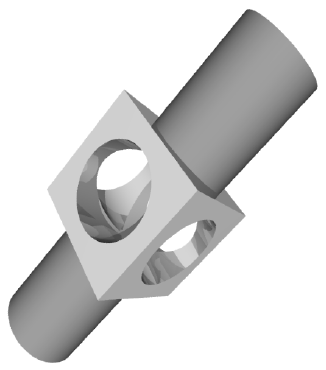
     Original CSG object with sharp edges.	Sampling (4102 points).

     EMST	Riemannian graph

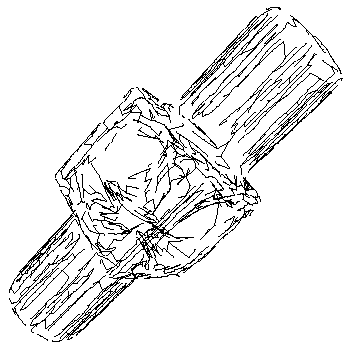
     Traversal order of orientation propagation.	Oriented tangent planes.

     Estimated signed distance (shown as p-z).	Cubes visited during contouring (intersect zero level-set).

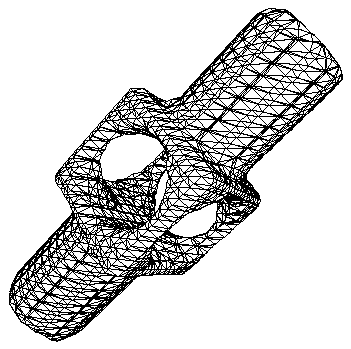
     Output of modified marching cubes.	Final surface after edge collapse.

      

     Comments:

     • One of the earliest methods dealing with "unorganized points" as an input.
     • Applicable to surfaces with boundaries (not closed).
     • The method criitically depends on the evaluation of a consistent (oriented) normal field, and as such, can be considered to solve in practice the problem of organized points.
     • Rounds-off corners due to poor tangent plane support.
     • Relatively high numerical complexity (dominated by the EMST computation which is O(n²).

     ---

     Surface reconstruction based on compactly supported radial basis functions

     Nikita Kojekine, Vladimir Savchenko and Ichiro Hagiwara

     In Geometric modeling: techniques, applications, systems and tools
     Kluwer Academic Publishers, pp. 218-231, 2004.

     Web links:

     • ACM portal
     • http://www.karlson.ru/csrbf/

     Abstract

     In this chapter the use of compactly-supported radial basis functions for surface reconstruction is described. To solve the problem of reconstruction or volume data generation specially designed software is employed. Time performance of the algorithm is investigated. Thanks to the efficient octree algorithm used in this study, the resulting matrix is a band diagonal matrix that reduces computational costs.

     ---

     Software Tools Using CSRBFs for Processing Scattered Data

     Nikita Kojekine, Ichiro Hagiwara and Vladimir Savchenko

     International journal "Computers & Graphics"
     published by Elsevier Science, vol. 27 (2), pp. 309-317, 2003.

     ---

     A Volumetric Method for Building Complex Models from Range Images

     Brian Curless and Marc Levoy,

     Proc. SIGGRAPH '96, New Orleans, LA, Pages: 303-312, 4-9 August 1996.
     (23rd annual conference on Computer graphics and interactive techniques)

     Web links:

     • Site at Stanford Graphics Lab: http://graphics.stanford.edu/papers/volrange/
     • ACM portal

     Abstract

     A number of techniques have been developed for reconstructing surfaces by integrating groups of aligned range images. A desirable set of properties for such algorithms includes: incremental updating, representation of directional uncertainty, the ability to fill gaps in the reconstruction, and robustness in the presence of outliers. Prior algorithms possess subsets of these properties. In this paper, we present a volumetric method for integrating range images that possesses all of these properties.

     Our volumetric representation consists of a cumulative weighted signed distance function. Working with one range image at a time, we first scan-convert it to a distance function, then combine this with the data already acquired using a simple additive scheme. To achieve space efficiency, we employ a run-length encoding of the volume. To achieve time efficiency, we resample the range image to align with the voxel grid and traverse the range and voxel scanlines synchronously. We generate the final manifold by extracting an isosurface from the volumetric grid. We show that under certain assumptions, this isosurface is optimal in the least squares sense. To fill gaps in the model, we tessellate over the boundaries between regions seen to be empty and regions never observed.

     Using this method, we are able to integrate a large number of range images (as many as 70) yielding seamless, high-detail models of up to 2.6 million triangles.

     ---

     Implicit Reconstruction of Solids from Cloud Point Sets

     Chek T. Lim - George M. Turkiyyah - Mark A. Ganter - Duane W. Storti
     University of Washington, Seattle, Washington 98195

     Proceedings of the third ACM symposium on Solid modeling and applications
     Salt Lake City, Utah, pp. 393-402
     ACM, 1995

     Web links:

     • http://www.me.washington.edu/~cdam/PEOPLE/CHEK/papers/acm_html/acm_all.html
     • ACM portal

     Abstract

     This paper describes a new technique that combines numerical optimization methods with triangulation methods for generating mathematical representations of solids from 3D point data. The solid representation obtained takes the form of an algebraic function whose level surface closely approximates the surface described by the data. The algebraic function is obtained via Implicit Solid Modeling, a constructive scheme for approximating Boolean volume set operations on implicitly defined primitive volumes, and is comprised of a blended union of spherical primitives. The parameters of the algebraic function are the spatial locations and radii of the spheres as well as the parameters that describe the blending of these primitives.

     Fitting an implicit solid model to a data set is formulated as a sequence of non-linear optimization problems of an increasing number of variables. The cost function we employ in these optimizations is a weighted combination of discrepancies in location (distance from points to boundary of reconstructed object), discrepancies in surface normals, and desired curvature characteristics of the reconstructed solid. Since a set of trivariate data points without any connectivity information is ambiguous, an infinite number of solids, in principle, can be constructed to fit them. Different characteristics of the solid can be specified through the cost function to create the most desirable interpretation of the data. The starting point of the optimization---corresponding to the starting configuration of the primitives---is determined by performing a 3D Delaunay triangulation on the data set, and is based on the locations and sizes of the resulting tetrahedra.

     The effectiveness of the algorithm is demonstrated through the reconstruction of several sample data sets, including a molar and a femur. Tradeoffs between accuracy and compactness of the representations are also examined.

     ---

     Marching Cubes: A High Resolution 3D Surface Construction Algorithm

     William E. Lorensen and Harvey E. Cline,

     Computer Graphics (Proceedings of SIGGRAPH '87), Vol. 21, No. 4, pp. 163-169.

     Web links:

     • The Marching Cubes Algorithm, by James Sharman.
     • Marching cubes, ESSI teaching project.
     • ACM portal : http://doi.acm.org/10.1145/37401.37422

     Patents:

     • United States Patent Number: 4,710,876, Date of Patent: Dec. 1, 1987, Inventors: Harvey E. Cline, William E. Lorensen, Assignee: General Electric Company, Title: "System and Method for the Display of Surface Structures Contained Within the Interior Region of a Solid Body", Filed: Jun. 5, 1985.
     • United States Patent Number: 4,885,688, Date of Patent: Dec. 5, 1989, Inventor: Carl R. Crawford, Assignee: General Electric Company, Title: "Minimization of Directed Points Generated in Three-Dimensional Dividing Cubes Method", Filed: Nov. 25, 1987.

     Abstract

     We present a new algorithm, called marching cubes, that creates triangle models of constant density surfaces from 3D medical data. Using a divide-and-conquer approach to generate inter-slice connectivity, we create a case table that defines triangle topology. The algorithm processes the 3D medical data in scan-line order and calculates triangle vertices using linear interpolation. We find the gradient of the original data, normalize it, and use it as a basis for shading the models. The detail in images produced from the generated surface models is the result of maintaining the inter-slice connectivity, surface data, and gradient information present in the original 3D data. Results from computed tomography (CT), magnetic resonance (MR), and single-photon emission computed tomography (SPECT) illustrate the quality and functionality of marching cubes. We also discuss improvements that decrease processing time and add solid modeling capabilities.

     ---

     Interpolating Implicit Surfaces from Scattered Surface Data Using Compactly Supported Radial Basis Functions

     Bryan S. Morse, Terry S. Yoo, David T. Chen, Penny Rheingans and K. R. Subramanian

     Proceedings of the International Conference on Shape Modeling & Applications
     IEEE Computer Society, pp. 89-98, Genova, Italy, May 2001.

     Web links:

     • IEEE/CS site
     • Conference: http://smi2001.ima.ge.cnr.it/

     Abstract

     We describe algebraic methods for creating implicit surfaces using linear combinations of radial basis interpolants to form complex models from scattered surface points. Shapes with arbitrary topology are easily represented without the usual interpolation or aliasing errors arising from discrete sampling. These methods were first applied to implicit surfaces by Savchenko, et al. and later developed independently by Turk and O'Brien as a means of performing shape interpolation. Earlier approaches were limited as a modeling mechanism because of the order of the computational complexity involved. We explore and extend these implicit interpolating methods to make them suitable for systems of large numbers of scattered surface points by using compactly supported radial basis interpolants. The use of compactly supported elements generates a sparse solution space, reducing the computational complexity and making the technique practical for large models. The local nature of compactly supported radial basis functions permits the use of computational techniques and data structures such as k-d trees for spatial subdivision, promoting fast solvers and methods to divide and conquer many of the subproblems associated with these methods. Moreover, the representation of complex models permits the exploration of diverse surface geometry. This reduction in computational complexity enables the application of these methods to the study of shape properties of large complex shapes.

     ---

     Volumetric Shape Description of Range Data using "Blobby Model"

     Shigeru Muraki

     Computer Graphics (SIGGRAPH' 91), Vol.25, No.4, pp. 227-235, 1991

     Web links:

     • ACM portal

     Abstract

     Recently in the field of computer vision, there have been many attempts to obtain a symbolic shape description of an object by fitting simple primitives to the range data of the object. In this paper, we introduce the "Blobby Model" for automatically generating a shape description from range data. This model can express a 3D surface as an isosurface of a scalar field which is produced by a number of field generating primitives. The fields from many primitives are blended with each other and can form a very complicated shape. To determine the number and distribution of primitives required to adequately represent a complex 3D surface, an energy function is minimized which measures the shape difference between the range data and the "Blobby Model". We start with a single primitive and introduce more primitives by splitting each primitive into two further primitives so as to reduce the energy value. In this manner, the shape of the 3D object is slowly recovered as the isosurface produced by many primitives. We have successfully applied this method to human face range data and typical results are shown. The method herein does not require any prior range segmentation.

     ---

     Multi-level Partition of Unity Implicits

     Yutaka Ohtake, Alexander Belyaev, Marc Alexa, Greg Turk, and Hans-Peter Seidel

     ACM TOG (Proc. SIGGRAPH 2003), 22(3):463-470, 2003.

     Web links:

     • http://www.mpi-sb.mpg.de/~ohtake/mpu_implicits/
     • ACM portal

     Abstract

     We present a shape representation, the multi-level partition of unity implicit surface, that allows us to construct surface models from very large sets of points. There are three key ingredients to our approach:

     1. piecewise quadratic functions that capture the local shape of the surface,
     2. weighting functions (the partitions of unity) that blend together these local shape functions, and
     3. an octree subdivision method that adapts to variations in the complexity of the local shape.

     Our approach gives us considerable flexibility in the choice of local shape functions, and in particular we can accurately represent sharp features such as edges and corners by selecting appropriate shape functions.

      

     Inputs:

     • Point set equipped with coherent unit normals (indicates the surface orientation), rescale to fit in a unit length bounding box.
     • Triangle mesh (i.e., with unit normals at vertices).

     Overview of approach:

     1. Octree subdivision of the bounding box containing data, where at each cell a piecewise quadratic function (the local shape function - LSF) fits the points in that cell. The LSF acts like a signed distance function. If the LSF approximation is not accurate enough, the cell is further divided.
         
     2. Blending near cell boundaries: In locations near the boundary of two or more cells, the LSF's are blended together according to weights from the partition of unity functions.
         

     Output:

     • Global implicit function given at the leafs of the octree subdivision by the partition of unity blending of the LSF.
     • The complexity of the method is output sensitive: i.e., it depends on the shape complexity of the reconstructed surface, rather than the number of input points.

      

     Summary

     Partition of Unity Approach

     • Permits to integrate locally defined approximants, using smooth local weights that sum up to one everywhere in the domain, into a global continuous approximation, with bounds on the local maximum error and convergence order.
        
     • Local functions for weights (piecewise (to allow for sharp features) quadratic (smoothness and ease of computation)) used:
       1. For approximation: quadratic B-splines
       2. For interpolation: inverse-distance singular weights
           

     Adaptive Octree-based Approximation

     • Radius for the weight functions is proportional to the diagonal of a cell: R = alpha . d
       • Time complexity is roughly quadratic in alpha. Larger values of alpha leads to smoother results.
          
     • Minimum number of points per cell: N_min = 15
       • kd-tree partitioning is used when growing a ball if the target N_min is not met in a cell.
          
     • A LSF Q(x) is built via least-squares.
       • When a cell is empty: compute the signed distance values.
       • When a cell contains data points: compute Taubin's local max-norm approximation error epsilon. If epsilon is greater that a user-supplied threshold e_0, the cell is further subdivided, and the fitting process refined for each smaller new cell.
          

     

     

      

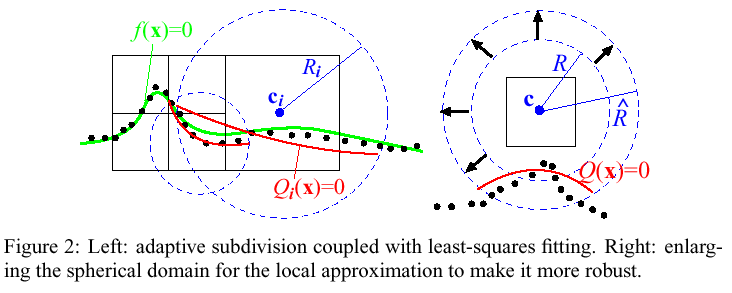
     Estimating Local Shape Functions (LSF):

     Function of the number of points in a cell and the distribution of normals, choose between one of three local approximations, where theta is the maximum angular deviation between an averaged normal and any individual normals in a given cell:

     1. a general 3D quadric (for large parts, unbounded or with multiple sheets, s.t. theta >= pi/2)
         
     2. a bivariate quadric polynomial in local coordinates (local smooth patch, s.t. theta < pi/2);
         
     3. a piecewise quadric surface that fits an edge or a corner (for sharp features; when N < 2N_min; perform clustering of normals in two (ridge) or three (corner) sets).
         

     

     

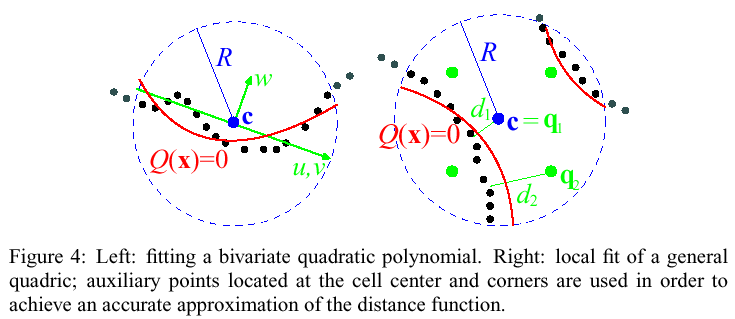
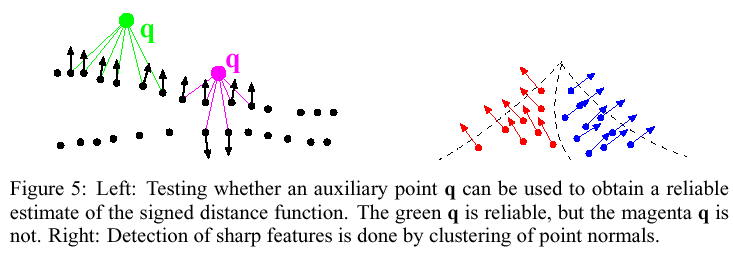
     Signed distance function evaluation:

     • Evaluated from the locally fitted kernel, for each cell at auxiliary points, q: cell corners and center.

      

     Pros:

     • Applicable to very large datasets.
     • Explicitly deals with sharp features.
     • CSG (Boolean) set operations are easy to implement: combine several MPU functions (possibly each with their own octree), and re-evaluate the global implicit function at each grid point.

     Cons:

     • Unclear if this method can easily process non-solids (with a clear-cut inside vs. outside; a priori it cannot).
     • Also, this is for organized data (rather than strictly unorganized), since a coherent normal field is required.
     • The global output distance function produced is inaccurate (not like an Euclidean distance transform; artifacts are visible in some results, esp. for offsetting shapes).

     ---

     Multiresolution Isosurface Extraction with Adaptive Skeleton Climbing

     Tim Poston, Tien-Tsin Wong and Pheng-Ann Heng

     Computer Graphics Forum, Vol. 17, No. 3, September 1998, pp. 137-148.

     Web link:

     • http://www.cse.cuhk.edu.hk/~ttwong/papers/asc/asc.html

     Abstract

     An isosurface extraction algorithm which can directly generate multiresolution isosurfaces from volume data is introduced. It generates low resolution isosurfaces, with 4 to 25 times fewer triangles than that generated by marching cubes algorithm, in comparable running times. By climbing from vertices (0-skeleton) to edges (1-skeleton) to faces (2-skeleton), the algorithm constructs boxes which adapt to the geometry of the true isosurface. Unlike previous adaptive marching cubes algorithms, the algorithm does not suffer from the gap-filling problem. Although the triangles in the meshes may not be optimally reduced, it is much faster than postprocessing triangle reduction algorithms. Hence the coarse meshes it produces can be used as the initial starts for the mesh optimization, if mesh optimality is the main concern.

     ---

     Modelling with Implicit Surfaces that Interpolate

     Greg Turk and James F. O'Brien

     ACM Transactions on Graphics, Vol. 21, No. 4, October 2002, pp. 855-873.

     Web link:

     • ACM portal: http://doi.acm.org/10.1145/571647.571650

     Abstract

     We introduce new techniques for modelling with interpolating implicit surfaces. This form of implicit surface was first used for problems of surface reconstruction and shape transformation, but the emphasis of our work is on model creation. These implicit surfaces are described by specifying locations in 3D through which the surface should pass, and also identifying locations that are interior or exterior to the surface. A 3D implicit function is created from these constraints using a variational scattered data interpolation approach, and the iso-surface of this function describes a surface. Like other implicit surface descriptions, these surfaces can be used for CSG and interference detection, may be interactively manipulated, are readily approximated by polygonal tilings, and are easy to ray trace. A key strength for model creation is that interpolating implicit surfaces allow the direct specification of both the location of points on the surface and the surface normals. These are two important manipulation techniques that are difficult to achieve using other implicit surface representations such as sums of spherical or ellipsoidal Gaussian functions ("blobbies"). We show that these properties make this form of implicit surface particularly attractive for interactive sculpting using the particle sampling technique introduced by Witkin and Heckbert.

     Our formulation also yields a simple method for converting a polygonal model to a smooth implicit model, as well as a new way to form blends between objects.

     ---

     Visualization, Analysis and Shape Reconstruction of Unorganized Data Sets

     H. Zhao and S. Osher

     Contributed chapter in S. Osher and N. Paragios, editors,
     Geometric Level Set Methods in Imaging, Vision and Graphics, Springer-Verlag, 2002

     Main goals:

     • Deal with arbitrary complexity (topologies), datasets (points, curves, surfaces, etc) and dimensions.
     • Provide approximate reconstructions permitting low cost visualization and analysis.
     • Provide multiscale processing for large unorganized datasets.

     Basic idea (solution):

     • Distance contours (level sets) of the input dataset are alike approximate offsets of the "shape" sampled by the inputs, which can be used to visualize, analyze disconnected components, characterize topological and geometrical information

     ---

     Fast Surface Reconstruction Using the Level Set Method

     Hong-Kai Zhao, Stanley Osher, Ronald Fedkiw
     Proceedings of IEEE Workshop on Variational and Level Set Methods in Computer Vision (VLSM'01),
     pp. 194-202, July, 2001, Vancouver.

     Main goal:

     • Surface reconstruction, analysis, deformation, for unorganized datasets, with low numerical complexity.

     Basic idea (solution):

     • Use (i) dynamic implicit surfaces (thus providing an explicit surface model, with smoothness and manifold properties) in the context of (ii) the level set method (to easily deal with arbitrary input datasets and topologies, giving resulting approximating surfaces which are close to the input dataset), providing a general framework to perform certain analysis tasks (e.g., connectivity, surface area, etc.) and deformation.

      

     Web sites:

     • http://math.uci.edu/~zhao/research/image/image.html
     • http://citeseer.ist.psu.edu/zhao01fast.html

     Abstract

     In this paper we describe new formulations and develop fast algorithms for implicit surface reconstruction based on variational and partial differential equation (PDE) methods. In particular we use the level set method and fast sweeping and tagging methods to reconstruct surfaces from scattered data set. The data set might consist of points, curves and/or surface patches. A weighted minimal surface-like model is constructed and its variational level set formulation is implemented with optimal efficiency. The reconstructed surface is smoother than piecewise linear and has a natural scaling in the regularization that allows varying flexibility according to the local sampling density. As is usual with the level set method we can handle complicated topology and deformations, as well as noisy or highly non-uniform data sets easily. The method is based on a simple rectangular grid, although adaptive and triangular grids are also possible. Some consequences, such as hole filling capability, are demonstrated, as well as the viability and convergence of our new fast tagging algorithm.

      

     Algorithmics summary:

     1. A fast algorithm to compute the distance function to an aribtrary dataset on rectangular grids is needed.
        • A variation of Danielsson's algorithm is proposed (no details).
           
     2. A good initial surface for a evolution propagation is needed.
        • To improve convergence speed a rough external frontier is sought.
        • Starting from outside (bounding box), march through the initial (unsigned) distance function (at grid points) towards lower distance values, until the temporary boundary starts breaking up (this gives the initial surface, with an inside and an outside, in the form of a polyhedron, ready for PDE evolution).
           
     3. Solve time dependent PDEs for a level set function.
        • This ressembles a snake (active surface under tension) system to converge to a smoother boundary, as pointed in the paper (end of section 2).
        • The reconstructed surface is more flexible in high density regions.
        • The evolution equation involves the mean curvature of the surface model and is non-linear.
        • Instead of explicitly tracking a surface model, solve a PDE for a level-set formulation to deform the surface model expressed in an implicit form (in a narrow-band arround the zero-level set).
        • Reinitialization is used to keep level-sets as a signed distance function (no cross-over).
        • Both a gradient flow and convection system of PDEs are proposed.
           

     Pros:

     • Applicable to various input types (points, curves, polygons, possibly other free-form sets).
     • Applicable to arbitrary topologies (but the recovery of holes is not clear, i.e., mixed with the active contour modeling).
     • Multi-resolution processing available.
     • Can be extended in principle to higher dimensional problems.
     • Smoothness enforced.
     • Can produce piecewise discrete manifolds (e.g., via marching cubes).
     • Surface operations, including Boolean, rendering, offsets, deformations, are available.
     • "Linear" numerical complexity: order N+M, where N is the number of grid points and M is the number of input samples.

     Cons:

     • Various parameters to set (in the snake-like model in particular) leading to varying results.
     • Complexity of the implementation.
     • Requires a grid at a certain resolution; possible memory issues.
     • Rounding-off of corners; sharp features such as ridges are often lost.
     • Assumes the object is closed or made of multiple closed parts.

      

     ---

     BACK

     Page created & maintained by Frederic Leymarie, 2004.
     Comments, suggestions, etc., mail to: leymarie@lems.brown.edu