|
|
|
|
|
Vertebra |
Polyballs |
Box and helix |
Last update: November 9, 2005
Publications on shape symmetry elicitation by Annick Montanvert, Dominique Attali, et al. :
BibTeX references.
Dominique Attali and J.-O. Lachaud
Computational Geometry: Theory and Applications, 2001. In press.
by Dominique Attali
& Annick Montanvert
Computer Vision &
Image Understanding, v 67, n 3, September 1997, pp.261-273
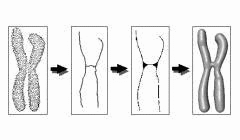
Skeletons provide a synthetic and thin representation of objects. Therefore, they are useful for shape description. Recent papers have proposed to approximate the skeleton of continuous shapes using the Voronoi graph of boundary points. An original formulation is presented here, using the notion of polyballs (we call polyball any finite union of balls). A preliminary work shows that their skeletons consist of simple components (line segments in 2D and polygons in 3D). An efficient method for simplifying 3D continuous skeletons is also presented. The originality of our approach consists in simplifying the shape without modifying its topology and in including these modifications on the skeleton. Depending on the desired result, we propose two strategies which lead to either surfacical skeletons or wireframe skeletons. Two angular criteria are proposed that allow us to build a size-invariant hierarchy of simplified skeletons.
|
|
|
|
|
Vertebra |
Polyballs |
Box and helix |
Let E be a finite set of points in R^n and p a point of E. The Voronoi region of p is the set of points of R^n closer to p than to any other element of E :
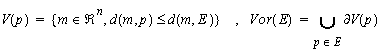
The Voronoi regions are convex polygons in 2D and convex polyhedra in 3D. The Voronoi graph of E, Vor(E), consists of the boundaries of the Voronoi regions of E. The Voronoi graph of n points can be computed in O( n log n + n^[N/2] ) in an N-D space.
It is the dual of the Voronoi grap and consists in a tessellation of the convex hull of E. It is made up of simplices whose circumscribed balls contain no other points of E. The simplices are triangles in 2D and tetrahedra in 3D for non-degenerate cases, i.e., s.t. no 4 points are co-circular in 2D or no 5 points are co-spherical in 3D. Like the Voronoi graph, it can be computed in O( n log n + n^[N/2] ) in an N-D space, and is denoted Del(E).
It is a set of simplices ] s1, s2, ..., sN [ s.t. the smallest ball passing through N points ( p1, p2, ..., pN ) contains no other points of E in its interior. It can be constructed from Del(E) by removing from it each N-face not intersecting its dual Voronoi edge. It can also be computed in O( n log n + n^[N/2] ) in an N-D space, and is denoted GG(E),
There are 4 different definitions :
Properties:
Thus, when the boundary of the polygonal approximation P is included in the Gabriel graph of E, the contour containment is verified and the skeletons SK0(P) & SK0(Pc) do not intersect the boundary of P.
Proposed "removing" criterion is scale-invariant and based on a generalized "bisector" angle.
A simplex T is removed from the current shape if the 2 following properties are verified:
When the simplex T is removed, its associated Voronoi vertex v and all the Voronoi elements going through v are also removed from the skeleton.
In 2D, only one type of triangle can be removed, which is associated with extremities of the skeleton and has one inner edge and 2 boundary edges: the hat triangle.
In 3D, 2 types of inner tetrahedra can be removed:
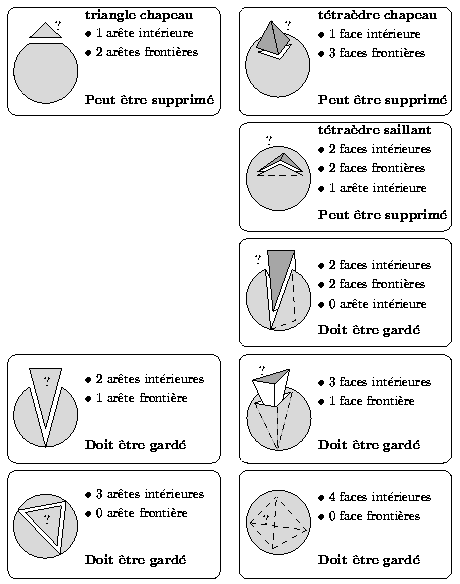
Fig.1 : Simplices Classification - Only hat trianges &
tetrahedra and salient tetrahedra
can be removed without altering the homotopy of the current shape.
Two different strategies are possible to simplify 3D skeletons:
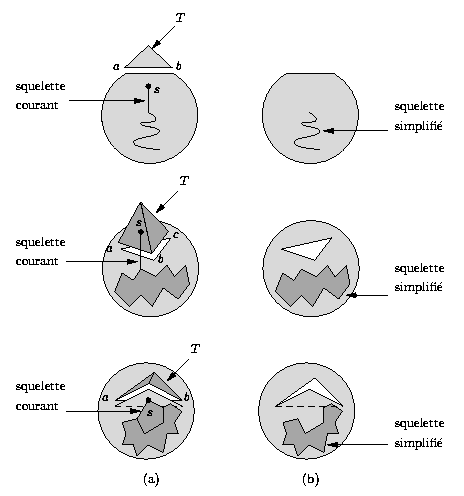
Fig.2 : Consequence on the skeleton of the removal of (i) a hat
triangle (2D),
(ii) a hat tetrahedron and (iii) a salient tetrahedron.
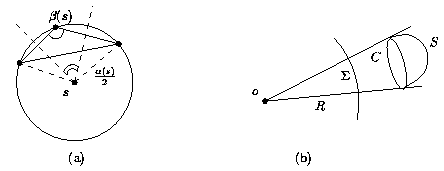
Fig.3: Bisector angle ß in 2D (a) and its generalization to 3D
(b).
|
|
|
|
|
|
|
1st column: initial polygonal approximation |
3rd column: initial skeleton |
In 2D, the skeleton of a polygon is made of straightline segments and portion of parabolic curves.
In 3D, the skeleton of a polyhedron is made of pieces of quadrics.
Polyball : Any finite union of balls.
Generating balls : minimum number of balls {Bi} that covers a polyball Y.
The skeleton of a polyball, in 2D or 3D, has a very simple structure. Its computation boild down to the computation of a Voronoi graph.
D.
Attali.
In Proc. of the 13th ACM Symposium on Computational Geometry,
pp.248-253,
Nice, France, June 1997.
Also in Special issue of Computational
Geometry: Theory and Applications, Vol. 10(4), pages 239-247,
July 1998.
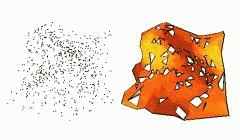 |
 |
In this paper, the problem of reconstructing a surface, given a set of scattered data points is addressed. First, a precise formulation of the reconstruction problem is proposed. The solution is mathematically defined as a particular mesh of the surface called the normalized mesh. This solution has the property to be included inside the Delaunay graph. A criterion to detect faces of the normalized mesh inside the Delaunay graph is proposed. This criterion is proved to provide the exact solution in 2D for points sampling a r-regular shapes with a sampling path e < sin (pi/8)r. In 3D, this result cannot be extended and the criterion cannot retrieve every face. A heuristic is proposed in order to complete the surface.
Keywords: Shape reconstruction; Interpolation; Delaunay graph; Voronoi graph; Normalized mesh; r-regular shape; Sample points.
E. Ferley, M.-P.
Gascuel, and D.
Attali
In Proc. of the 2nd international workshop on Implicit Surfaces,
pp.127-142,
Eindhoven, the Netherlands, October 1996
Also in Computer Graphics Forum, Vol. 16, No 5., pages 283-293,
December 1997.
 |
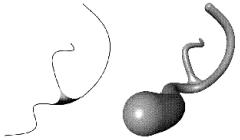 |
We present a new method for the implicit reconstruction of branching shapes from a set of scattered data points. The method is based on the computation of a geometric skeleton inside the data set. This skeleton is simplified in order to filter noise and converted into skeletal elements -- a graph of interconnected curves -- that generate an implicit surface. We use Bézier triangles as extra skeletal elements to perform bulge free blends between branches while controlling the blend extent. This leads to a smooth implicit representation of the shape, directly computed in a purely geometric way.
by Dominique
Attali & Annick Montanvert
In Proc. of the International Conference on Image Processing (ICIP'96),
Volume III, pp.13-16, Lausanne, Switzerland, September 1996
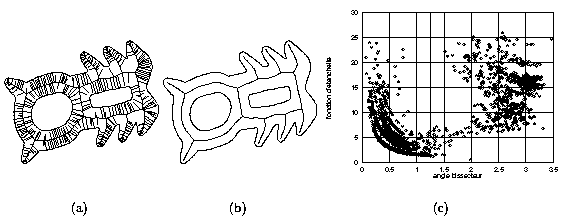
Let the shape X be sampled as a set of points { qi }(0 < i < n+1), where each sample point can be written as the sum : qi = pi + ei , where pi is the "true" boundary coordinate of boundary point of X and the vectors ei represent additive noise.
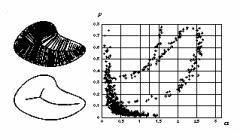
Thickness : radius rho(s) at a skeletal point s of the maximal ball centered on s.
Bisector angle : angle ß(s) at a "simple" skeletal point s, taken between s and the 2 boundary points p0 & p1 given by the intersection with the boundary of X of the maximal ball centered at s. The bisector angle is s.t.:
Consider the parameter graph, where skeletal vertices are plotted according to rho(s) against ß(s). In 2D, noise shows in this graph as strata of scattered points near the origin and the axes, along hyperbolas (the strata are due to quantization which forbids certain range of values for the radius of the maximal balls - discretization effect on the distance map). Thresholds on the radius and bisector angle are given by cutting off the hyperbolically distrbuted scattered data from the parameter graph. This defines a rectangular region of interest in the upper-right side of this graph.
 |
 |
This local characterization of noise does not translate to a practical method in 3D. See the PhD thesis of Attali (Ch.6) or the recent paper "Computing & Simplifying 2D & 3D Continuous Skeletons" (section on "3D Skeleton Simplification").
PhD thesis by Dominique Attali
(in French)
Joseph Fourier University - Grenoble 1, France
13 October 1995.
Now with the "Ecole Nationale Supérieure d'Ingénieur Electricien de Grenoble" (ENSIEG), France.
D. Attali, P. Bertolino, and A. Montanvert
In 12th International Conference on Pattern Recognition (ICPR),
pp.626-628,
Jerusalem, Israël, October 1994
Page created & maintained by Frederic Leymarie,
1998-2005.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu