March 22, 1999

Publications by Prof. William Warntz (retired from Harvard Grad. School of Design) et al. :

• Geographical systems & systems of geography: Essays in honour of William Warntz, 1988.
• "Geography and the Properties of Surfaces" Series:
  • Concepts and Applications - Spatial Order, Paper #1, by W. Warntz & M. Woldenberg, May 1967.
  • The Sandwich Theorem - A Basic One, Paper #44, by W. Warntz et al., June 1971.

BibTeX references.

Ch.1 - The Origins of Systems Thinking in Geography

William J. Coffey

Ch.2 - The Mushroom Shape

William Bunge

Check work by William Prager, from Brown, DAM, on "pattern of networks" (similar to 2D shock graphs). Look for A "Progress Report, #2, from DAM, Brown U., entitled "Derivationn of Results Stated in rogress Report No.1", 1956.

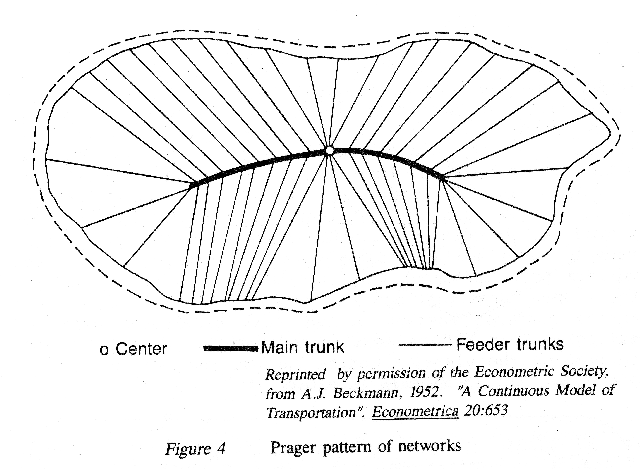
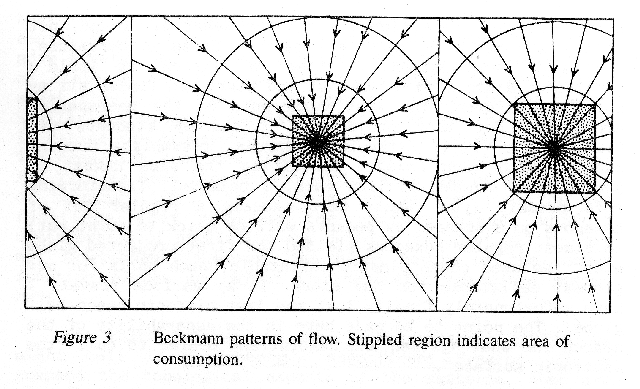
Ch.3 - Nodal Hierarchies & the Concept of Survival

Allen K. Philbrick

Ch.4 - Structural Evolution in Spatial Systems: Macrogeographical Explorations Beyond the Realm of Stability

Roger W. White

Ch.5 - The Quadratic Transportation Problem as a Model of Spatial Interaction Patterns

Waldo R. Tobler

Ch.6 - Spatial Interaction Models Incorporating Serial Dependency Effects

James Pooler

Ch.7 - A Model of Metropolis: The City as the Market

Oscar Fisch

Ch.8 - Geometry and Topology, Causality and Explanation: Hierarchical Description of Geographic Patterns

David M. Mark

Ch.9 - Microgeographic Determination of Optimality in Mammalian Trees

Michael J. Woldenberg

Ch.10 - The Invertibility of Distance Matrices

Michael F. Goodchild & David M. Mark

Relates to Kriging and the interpolation of height surfaces (Monge).

Ch.11 - Least Cost Paths Through Space

Terence R. Smith & Pascal M. Gahinet

Ch.12 - Expert Systems and Systems of Experts

Nigel Waters

Ch.13 - Patterns of Contact and Influence in the Life of a Spatial Scientist: William Warntz

Donald G. Janelle & Barabara Janelle

Includes a complete bibliography of William Warntz.

A. Demonstration of a General Property of Closed Surfaces

B. An Additional Graphical Portrayal

C. Contour Lines

D. Varying the Contour Interval & Singular Points

E. Singular Points & Lines

F. Hills and Dales and Territories

G. Surfaces and the Mathematical Functions of Three Variables

H. Multiple Passes and Pales

I. Hills, Dales, Territories & General Topological Considerations

J. The Indicatrix

K. Surfaces, Flows, and Dimensions

A. Exponential & Allometric Growth as Most Probable States for Open Systems

B. On the Ordering of Tree-like Course Lines on Surfaces: The Example of the River

C. On the Ordering of Tree-like Course Lines on Surfaces: The Example of the Mountain Glaciers

D. On the Ordering of Points in Areas: The Example of a Central Place System for Human Activities

E. On the Similarities & Differences Between Tree-like & Web-like Open Systems

F. A Theory of Geomorphic Cyclical Evolution Based on the Graded Profile

Sandwich Theorem:

• Given any 3 sets in space, each of finite outer Lebesgue measure, there exists a plane which bisects all 3 sets, in the sense that part of each set which lies on one side of the plane has the same outer measure as the part of the same set which lies on the other side of the plane.