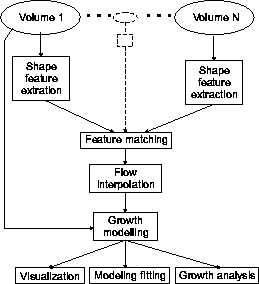
Fig.1 : Flow chart of the algorithms involved in the growth analysis.
Last update, Jan. 2, 2003
by Roman Durikovic et al. :
by Per Rønsholt Andresen et al. :
BibTeX references.
S. Czanner, R. Durikovic, H. Inoue , The University of Aizu
IEEE 17th Spring Conference on Computer Graphics (SCCG
'01), pp. 139-146,
April 25 - 28, 2001, Budmerice, Slovakia.
Web links:
The growth of the brain of human embryo is changing through a long time in the body of mother. So it is very difficult to observe and to understand that process. Therefore, the embryologists found the realistic human organ models and animations necessary for their studies. But to create the realistic human embryo brain models and to do the animations it requires an appropriate methodology. The aim of this paper is to present a developing methodology based on the functional representation and the convolution of the surfaces [4,5,6 ]. We employed this to create a growth simulation of the human embryo brain. The idea of this technique is the following. As a first step the 2D central skeleton is created from an artistic drawing and then the 3D skeleton is modeled by adding the thickness. As the next step, the skeletons representing key-frame models are used to create an animation. At the end the gap between the key-frame models is filled by the suitable interpolation techniques and finally the animation is composed.
Index Terms: human embryo, brain, convolution surfaces, F-rep, geometric modeling, blending, skeleton, morphing, animation.
Per Rønsholt Andresen
IMM-PhD-1999-65
3D-Lab, School of Dentistry, Technical University of Denmark, Denmark
e-mail: pra@imm.dtu.dk , URL: http://www.imm.dtu.dk/~pra
Based on the work of Thirion et al. (INRIA - Epidaure Project)
Extremal lines:
Extremal points:
Extremal mesh:
Computations based on the work of the INRIA folks: considers differentials on iso-surfaces. This is proposed instead of first fitting some surface model to the data.
[ TOP ]
Per Rønsholt Andresen, Mads Nielsen and Sven Kreiborg
3D-Lab, School of Dentistry, University of Copenhagen, Denmark
Department of Mathematical Modelling, Technical University of Denmark,
Denmark
e-mail: pra@imm.dtu.dk , URL: http://www.imm.dtu.dk/~pra
Published at MICCAI'98 , MIT, Oct. '98, pp.710-719.
From a set of temporally separated scannings of the same anatomical structure we wish to identify and analyze the growth in terms of a metamorphosis. That is, we study the temporal change of shape which may provide an understanding of the biological processes which govern the growth process. We subdivide the growth analysis into growth simulation, growth modelling, and finally the growth analysis. In this paper, we present results of growth simulation of the mandible from 3 scannings of the same patient in the age of 9 months, 21 months, and 7 years. We also present the first growth models and growth analyzes.
Introduction
Local Shape Features
Feature Matching
Flow Interpolation
Growth Modeling
Growth study is divided into:
In contrast to normal biological tissue growth, bone grows only on the surface. The interior is rigid and does not change shape. The growth of a bone can be subdivided into deposition (adding bone) and resorption (removal of bone). Because the deposition and resorption happen all over the surface of the bone at different speeds, this results in non-linear growth.
Homologous points are followed over time, defining a spatio-temporal vector field (the growth vector field or just vector field or flow field). The goal of growth simulation is the identification of the spatio-temporal vector field. Many different vector fields will satisfy the constraints given by the data and the definitions of homologous points. Thus a growth model (or interpolation model) must be used for the determination of a unique vector field.

Fig.1 : Flow chart of the algorithms involved in the growth analysis.
The growth vector fields link homologous points, or points of equivalent morphology. We define equivalence classes of points on a surface. The local shape (properties up to a rigid transformation) of a surface is totally characterized by the principal curvatures (k1, k2, s.t. k1 > k2) and their derivatives in the coordinate system defined by the principal directions (t1, t2).
Since the bone topology is not changing in our studies, we may model the growth process by a 3D diffeomorphism (a 1-to-1 differential mapping). This corresponds to D'Arcy Thompson classical methods of transformations. The principal curvatures and directions will in general change when exposed to this non-linear diffeomorphism, and cannot directly be used for registration. However, certain shape singularities are structurally stable in the sense that they cannot be removed by an infinitesimal perturbation, but they will in general change topology under finite perturbations. Here, we give a list of some stable shape features (Table 1).
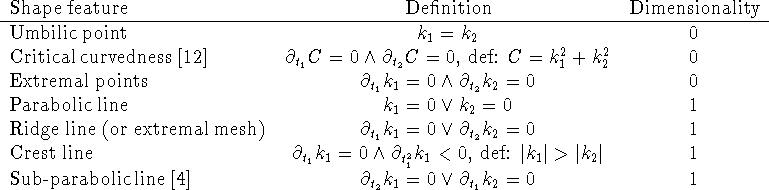
Table 1 : Shape features (singularities) with dimension < 2.
We work with the extraction and matching of ridge lines in a scale-space setting. The ridge lines (or extremal mesh) can be partitioned into four types corresponding to respectively maximum or minimum in k1 and k2. We use the maxima in (the absolute value of) both k1 and k2.
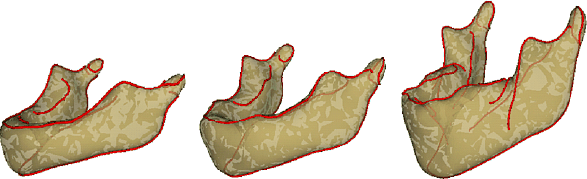
Fig.2 : Crest lines on the 3 smooth mandibles at 9 months, 21
months, and 7 years old.
As features we will only consider the lines with maximally k1 (crest-lines) and maximally k2 (here, called k2-max lines) in the extremal mesh. The overall framework follows the ideas of G. Subsol, J.-P. Thirion, and N. Ayache ("A general scheme for automatically building 3D morphometric anatomical atlases: application to a skull atlas". Medical Image Analysis, 1998. To be published.) First we need the crest lines and k2-max lines for each dataset at scale 3.0 (matching) and 1.0 (localization).
The crest lines at scale 3.0 are registered pairwise (here, it means only the neighboring dataset), and initial vector fields are calculated. The k2-max lines are then deformed according the initial vector fields. From the 2 sets of matches (one from the crest-lines, the other from the k2-max lines) final vector fields are calculated. This procedure is repeated for scale 1.0, but the lines are initially deformed according to the the final vector fields for scale 3.0.
The steps in the registration are always the same. First moment-registration, then 2 first order polynomial deformations, followed by 2 second order polynomial deformations. Lastly a totally non-rigid deformation is applied (all points on the lines move freely). For all the registration methods (including the non-rigid) they must satisfy the restriction that the deformation must be a 3D diffeomorphism.
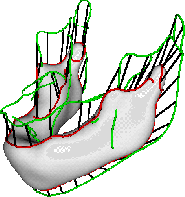
Fig.3 : The final matches (lines in black) between 2 sets of crest
lines. The crest lines on the 21 months and 7 years mandible are red
and green, respectively. It is seen that the condyles on the two
mandibles are matched together. For visual clarity only every eighth
match is shown.
Interpolation will be constrained as follows:
Assume that the covariance function C(x,x') is known; it expresses the covariance of the vector field values in two points x and x'. Typically, the closer the points are, the more correlated their data values are assumed to be. An interesting aspect is that if this covariance defines a distribution of functions, and if
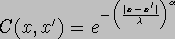 ,
,
some well-known function classes appear with probability 1, for different choices of alpha:
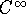 .
.
Given the covariance function C(x,x') and an expression of the belief in data as the assumed variance of data values r², we can make a maximum likelihood estimation (MLE) of f(x) as:

where w(x, x') is a vector containing wi = C(x,xi), and Q is a matrix containing
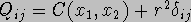 .
.
The intuitive interpretation of the introduction of Q¯¹ is that, prior to the regularizations based on the covariance function, an inverse filtering is performed to make the samples uncorrelated. In terms of scale-space, we might say that we have data given at some scale lambda. To interpolate, we first perform a deblurring to scale zero, then interpolate and then blur back to the current scale. This method satisfies all criteria when alpha = 1 (Brownian motion) and r = 0. Lambda can be chosen freely, so as to adjust the smoothness of the interpolated vector field. In Figure 4, the deformation of the mandible is shown as it is transported along the deformation vector field.
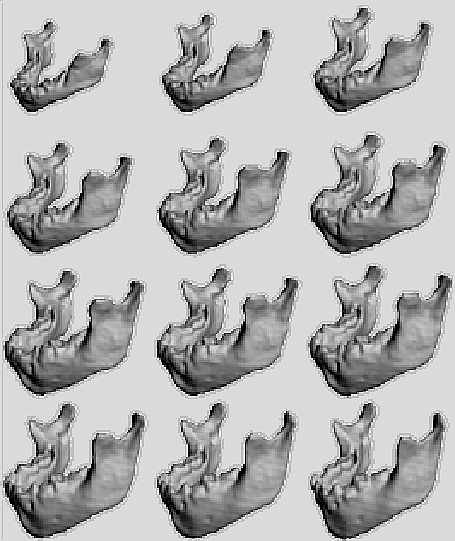
Fig.4 : Result of deformations on the 7 years mandible using a 2nd
order polynomial model. The top left & right images are the
deformation at 9 months and 21 months, respectively. The bottom right
image is the original 7 years old mandible.
We have the general model  ,
, 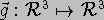 (for fixed t), and the 3D volumes
(for fixed t), and the 3D volumes 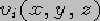 ,
where
,
where ![]() is the parameters for
is the parameters for ![]() ,
and (x,y,z) defines a point in Euclidean 3D space. t is
the time. i = {1, ... , n}is an index,
where n is the total number of volumes.
,
and (x,y,z) defines a point in Euclidean 3D space. t is
the time. i = {1, ... , n}is an index,
where n is the total number of volumes. ![]() is the time at the ith scan. We need to pick a reference
volume, let's say
is the time at the ith scan. We need to pick a reference
volume, let's say ![]() .
All deformations will then be applied to this set, i.e. a simulated
volume at time t is given by
.
All deformations will then be applied to this set, i.e. a simulated
volume at time t is given by 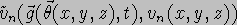 or
or ![]() for short. We want to solve the problem:
for short. We want to solve the problem:
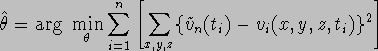
Note, when having  ,
the actual deformation on the volume
,
the actual deformation on the volume ![]() from time
from time ![]() to t, can always be made by a linear deformation (we just pick
the straight line between the two points
to t, can always be made by a linear deformation (we just pick
the straight line between the two points ![]() and
and 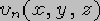 .
.
In general, this leads to a non-linear optimization problem, but if we pick models, linear in the parameters, regression analysis can be used. Linear models :
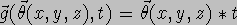
have been used in previous work. This model has the drawback that a
point, p, can only grow in the direction of the vector ![]() .
Furthermore, the growth of the mandible is not linear. The simplest
non-linear model is then a polynomial model:
.
Furthermore, the growth of the mandible is not linear. The simplest
non-linear model is then a polynomial model:
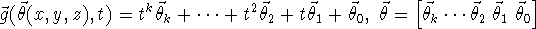
In practice, the growth speed is not constant, but this can be handled by the model by re-parametrizing the time variable, t.
Other possible models include logarithmic spirals and power functions, known from the theory of growth or spatially constrained models.
[ TOP ]
Mads Nielsen and Per Rønsholt Andresen
ICIP'98
Page created & maintained by Frederic Leymarie,
1999-2003.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu