Last update, August 1, 2004

BACK

Publications by

• Estimating the in/out function of a surface represented by points, 2003.
• Volume Warping for Adaptive Isosurface Extraction, 2002.
• Building a digital model of Michelangelo's Florentine Pieta, 1999 & 2002.
• The Ball-Pivoting Algorithm for Surface Reconstruction, 1999.
• Computing Consistent Normals and Colors from Photometric Data, 1999.
• Implicit Simplicial Models I: Adaptive Curve Reconstruction, 1996.
• Parameterized Families of Polynomials for Bounded Algebraic Curve and Surface Fitting, 1994.
• Curve and Surface Smoothing Without Shrinkage, 1994.
• Distance approximations for rasterizing implicit curves, 1994.
• Recognition and Positioning of Rigid Objects using Algebraic and Moment Invariants, Ph.D., 1990.

BibTeX references.

More references:

• http://mesh.brown.edu/taubin/publications.html

Web links:

• ACM portal

We present a method to estimate the in/out function of a closed surface represented by an unorganized set of data points. From the in/out function, we compute an approximation of the signed distance function to a surface M whose sampling are given by this set of points. The procedure correctly detects the interior and the exterior of M, even if M is multiply connected. The representation of the signed distance function combines the advantages of two previously known schemes, "Implicit Simplicial Models" and "Adaptively Sampled Distance Fields", incorporating new features deriving from the concept of a Binary Multitriangulation.

Inputs:

• Unorganized (without normals) point samples of a closed surface (i.e., bounding a solid.

Outputs:

• Simplicial decomposition of a bounding box s.t. each grid vertex has sign +/- (out/in).
• Combines Implicit Simplicial Models with Adaptively Sampled Distance Fields.

Algorithm:

1. Iteratively subdivide a bounding box for the input samples into a set of tetrahedra based on a PCA (plane fitting).
2. These simplicial cells are then oriented by minimizing a global cost function for their consistent alignment (prescribing signs at cell vertices). This is performed via a simulated annealing solver (the most complex part of the algorithm).
3. Signed distance values are then approximated at cell vertices.
4. A polygonizer is applied to extract the zero level-set of the distance function.

Web links:

• ACM portal

Polygonal approximations of isosurfaces extracted from uniformly sampled volumes are increasing in size due to the availability of higher resolution imaging techniques. The large number of primitives represented hinders the interactive exploration of the dataset. Though many solutions have been proposed to this problem, many require the creation of isosurfaces at multiple resolutions or the use of additional data structures, often hierarchical, to represent the volume.We propose a technique for adaptive isosurface extraction that is easy to implement and allows the user to decide the degree of adaptivity as well as the choice of isosurface extraction algorithm. Our method optimizes the extraction of the isosurface by warping the volume. In a warped volume, areas of importance (e.g. containing significant details) are inflated while unimportant ones are contracted. Once the volume is warped, any extraction algorithm can be applied. The extracted mesh is subsequently unwarped such that the warped areas are rescaled to their initial proportions. The resulting isosurface is represented by a mesh that is more densely sampled in regions decided as important.

Web links:

• Pietà Project @ IBM
• IEEE explore

We present the methodology we used to acquire the data and construct a computer model of Michelangelo's Florentine Pieta with enough detail and accuracy to make it useful in scientific studies. We describe the project to acquire and build the 3D model. The work we describe is unique in that an art historian, not a technologist, conceived and specified the project. Our goal wasn't simply to produce the statue's model but also to provide the art historian with material and tools to enable him to answer his own research questions. The project gave us the opportunity to explore the value of 3D scanning and visualization in a nontechnical discipline, art history. The project's second goal was to develop scanning technology accessible to other cultural heritage projects both in terms of cost and usability

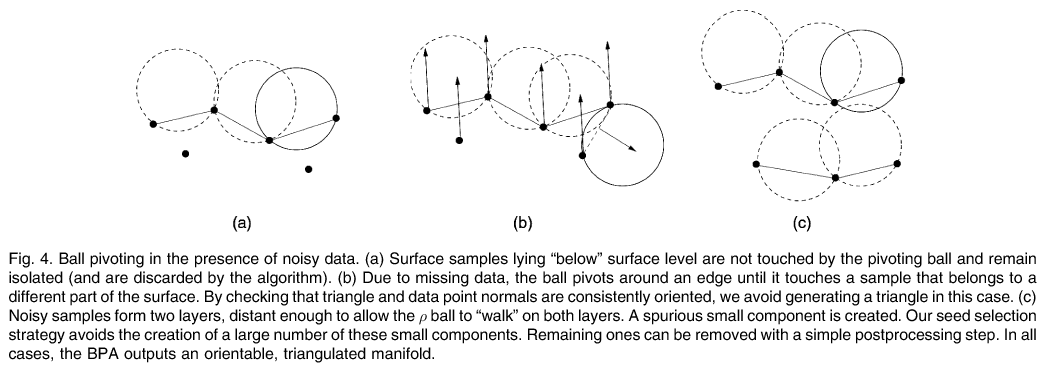
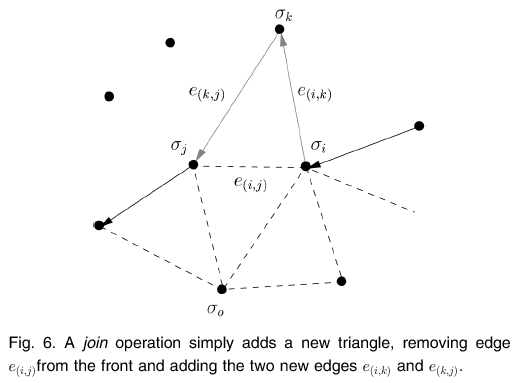
The Ball-Pivoting Algorithm (BPA) computes a triangle mesh interpolating a given point cloud. Typically, the points are surface samples acquired with multiple range scans of an object. The principle of the BPA is very simple: Three points form a triangle if a ball of a user-specified radius _ touches them without containing any other point. Starting with a seed triangle, the ball pivots around an edge (i.e., it revolves around the edge while keeping in contact with the edge's endpoints) until it touches another point, forming another triangle. The process continues until all reachable edges have been tried, and then starts from another seed triangle, until all points have been considered. The process can then be repeated with a ball of larger radius to handle uneven sampling densities. We applied the BPA to datasets of millions of points representing actual scans of complex 3D objects. The relatively small amount of memory required by the BPA, its time efficiency, and the quality of the results obtained compare favorably with existing techniques.

Index Terms: 3D scanning, shape reconstruction, point cloud, range image.

Assumptions:

1. Samples are distributed over the entire surface with a spatial frequency greater than or equal to some application-specified minimum.
2. Estimates if the surface normal is available at each sample.

The ouput mesh is a manifold subset of an alpha-shape of the point set.

Computing a 3D Delaunay triangulation can be prohibitively expensive and can lead to numerical instability.

Two sources of errors in scanning systems:

1. registration
2. along the sensor line of sight

[ TOP ]

[ TOP ]

Web links:

• ACM portal
• IEEE explore

Parametric deformable models have been extensively and very successfully used for reconstructing free-form curves and surfaces, and for tracking nonrigid deformations, but they require previous knowledge of the topological type of the data, and good initial curve or surface estimates. With deformable models, it is also computationally expensive to check for and to prevent self-intersections while tracking deformations. The Implicit Simplicial Models that we introduce in this paper are implicit curves and surfaces defined by piece-wise linear functions. This representation allows for local deformations, control of the topological type, and prevention of self-intersections during deformations. As a first application, we also describe in this paper an algorithm for two-dimensional curve reconstruction from unorganized sets of data points. The topology, the number of connected components, and the geometry of the data are all estimated using an adaptive space subdivision approach. The main four components of the algorithm are topology estimation, curve fitting, adaptive space subdivision, and mesh relaxation.

N-dimensional smoothing of piece-wise linear shapes that roughly retains the original size and preserve topology. It is a linear low-pass filter that removes high-curvature variations (in lieu of high frequencies).

[ TOP ]

Web links:

• ACM portal
• IEEE explore

Interest in algebraic curves and surfaces of high degree as geometric models or shape descriptors for different model-based computer vision tasks has increased in recent years, and although their properties make them a natural choice for object recognition and positioning applications, algebraic curve and surface fitting algorithms often suffer from instability problems. One of the main reasons for these problems is that, while the data sets are always bounded, the resulting algebraic curves or surfaces are, in most cases, unbounded. In this paper, the authors propose to constrain the polynomials to a family with bounded zero sets, and use only members of this family in the fitting process. For every even number d the authors introduce a new parameterized family of polynomials of degree d whose level sets are always bounded, in particular, its zero sets. This family has the same number of degrees of freedom as a general polynomial of the same degree. Three methods for fitting members of this polynomial family to measured data points are introduced. Experimental results of fitting curves to sets of points in R² and surfaces to sets of points in R³ are presented.

In this article we present new algorithms for rasterizing implicit curves, i.e., curves represented as level sets of functions of two variables. Considering the pixels as square regions of the plane, a "correct" algorithm should paint those pixels whose centers lie at less than half the desired line width from the curve. A straightforward implementation, scanning the display array evaluating the Euclidean distance from the center of each pixel to the curve, is impractical, and a standard quad-tree-like recursive subdivision scheme is used instead. Then we attack the problem of testing whether or not the Euclidean distance from a point to an implicit curve is less than a given threshold. For the most general case, when the implicit function is only required to have continuous first-order derivatives, we show how to reformulate the test as an unconstrained global root-finding problem in a circular domain. For implicit functions with continuous derivatives up to order k we introduce an approximate distance of order k. The approximate distance of order k from a point to an implicit curve is asymptotically equivalent to the Euclidean distance and provides a sufficient test for a polynomial of degree k not to have roots inside a circle. This is the main contribution of the article. By replacing the Euclidean distance test with one of these approximate distance tests, we obtain a practical rendering algorithm, proven to be correct for algebraic curves. To speed up the computation we also introduce heuristics, which used in conjunction with low-order approximate distances almost always produce equivalent results. The behavior of the algorithms is analyzed, both near regular and singular points, and several possible extensions and applications are discussed.

BACK      TOP     

Page created & maintained by Frederic Leymarie, 2000-4.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu