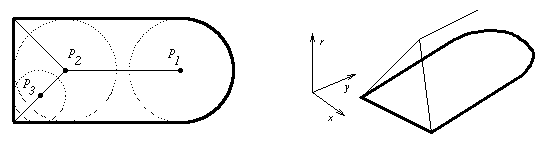
Figure 1 : Maximal inscribed balls.
These definitions are given relative to two-dimensional objects. Extension to three-dimensional objects for each is natural, except as noted.
There are many equivalent definitions of the MAT. We give two here which are particularly useful for our application of MAT to boundary conversion.
One definition is in terms of maximal inscribed discs, discs which are completely contained inside the object and which are contained in no other such disc. The medial axis (MA) of an object, also referred to in the literature as the skeleton, is the closure of the locus of the centers of all maximal inscribed discs. The medial axis transform (MAT) is the medial axis and, for each point on the medial axis, the radius of the maximal inscribed disc centered there. Thus for two-dimensional objects, the MAT is actually a three-dimensional representation: x,y-coordinates for the location of the center of the disc, and an r-coordinate for the radius of the disc. On the left in Figure 1 is a boundary and its MA, along with some of the maximal discs. On the right, the MAT corresponding to the figure is shown.
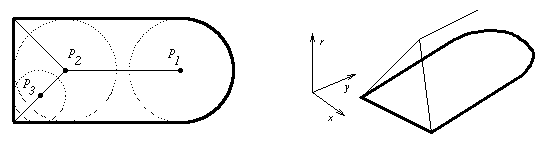
Figure 1 : Maximal inscribed balls.
The second definition is from the theory of cyclographic maps. Starting with an oriented curve C in the xy-plane, a ruled surface is formed by the set of all lines through the curve which make a 45 degree angle with the xy-plane and whose projection onto the xy-plane is normal to the curve at the intersection point. The line should increase towards the interior of C. For a given point (x,y) in the plane, there might be multiple values of z such that (x,y,z) lies on the surface. If (x,y) is in the interior of C, take the point with positive z value nearest to the xy-plane, and if it is exterior to C, take the point with negative z-value nearest to the xy-plane. The surface so generated is single-valued and defined over the xy-plane. Each point (x,y,z) on this surface gives the distance from (x,y) to C, hence it is referred to as the distance surface of C. The distance surface has singularities at the points where two or more of the generating lines meet. The curves given by the closure of these singularities comprise the MAT. Figure 2 shows this surface for the object of Figure 1, with the boundary curves and the MAT curves highlighted.
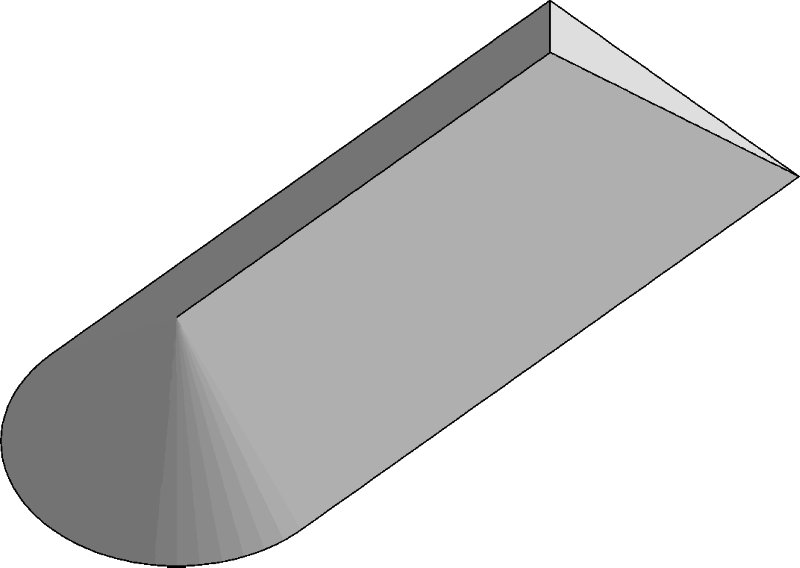
Figure 2 : Cyclographic map as a Distance Surface.
The maximal disc definition provides a natural way to distinguish between types of MA points. The distinction is based on the number of contiguous touchings the disc centered at the point has with the boundary. A disc can touch with point contact, that is, a single boundary point touches a single point on the disc boundary, or with finite contact, in which a contiguous arc of points on the disc touches a segment of the boundary. Either type is considered a single touching. The order of a point is the number of touchings that the disc related to an MA point has with the boundary. An MA point of order one is an end point. Normal points are MA points of order two, and branch points are points with three or more boundary touchings. In Figure 1, p1 is an endpoint, p2 is a branch point, and p3 is a normal point. The term ``finite contact'' seems a bit incongruous, since this type of contact actually is the only contact involving a non-finite number of points. Historically, Blum introduced this term as shorthand for ``the disc contacts the boundary in a finite length of arc'', and we follow his terminology here.
For three-dimensional objects, the MA points can be subdivided into end points, normal points, and branch points, using a similar criteria of number of contiguous touchings of the the sphere with the boundary as in the two-dimensional case. Now, however, finite contact can mean a curve of the sphere contacts the boundary or a surface patch on the sphere contacts the boundary. Also, branch points and normal points are no longer separated in the way they were in the two-dimensional case. Instead, branch points and endpoints can be contiguous along a curve. Figure 3 shows a simple rectangular box on the left and its MA on the right. The branch curves occur where the planar sections intersect, and the end point curves run along corners of the box.
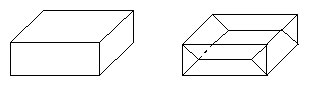
Figure 3 : MA in 3D of a box.
In the theoretical development for two-dimensional objects, we require that the objects under consideration satisfy certain reasonable topological and geometric constraints.
A 2D object O is simple if the following are satisfied:
The requirement of bounded variation means simply that any line in the plane intersects the curve in finitely many points, or finitely many segments in case the line should coincide with the curve in a region. This eliminates boundary curves which fluctuate infinitely often.
This definition is not overly restrictive, since most objects of interest in design situations satisfy these requirements inherently. Simple objects may have a finite number of interior voids, so that although the MAT will be connected, it need not be simply connected. Further, since each boundary loop is piecewise curvature continuous, the boundary curves are all locally parameterizable except possibly at points of connection between segments.
A boundary direction vector or direction vector for short, is any vector connecting an MA point to one of its related boundary point. Notice that because the maximal inscribed disc is in general tangent to the boundary, direction vectors are in general normal to the boundary at the related boundary point.