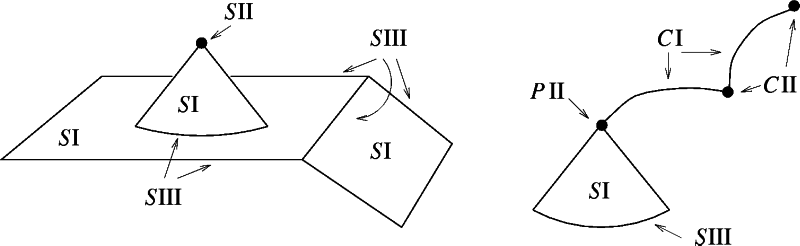
Figure 1 : The various types of MAT point in 3D.
One important property of the MAT is its uniqueness. That is, given any boundary there is exactly one MAT related to it, and given any MAT, there is exactly one boundary from which it could have been derived. Wolter has shown that the boundary and interior of a simple object can be retrieved from the MAT by taking the union of all the maximal spheres defined by the MAT. Note that this implies that for a given MAT, the boundary related to it must be closed.
N.B.: This is too restrictive; open boundaries, or even scattered points in 3D space can have associated MATs. The latter will be connected although the object boundaries are not.
Furthermore, from this we immediately have the following 2 properties:
N.B.: The Union Property requires some constraints on the set union operation. The MATs probably have to intersect.
Based on the properties for simple objects and tangency considerations arising from the cyclographic hypersurface definition of the MAT, we now make the following assumptions about the MATs M we consider for the conversion theory.
These assumptions allow us to sort the MAT points into groups, each of which is handled differently in the conversion process, since the conversion will be based on the tangent planes and vectors at a point. The various types of points are displayed in Figure 1.

Figure 1 : The various types of MAT point in 3D.
Any point p of M falls into one of the following categories:
The technique used to establish the theory for converting from the 3D MAT to the boundary is similar to that for 2D. That is, for each MAT point p, we wish to find all boundary points related to p based solely on p itself and complete tangent information of the MAT at p. Using the classification of MAT points laid out in the previous section, for each type of MAT point, we demonstrate how to locate all of the related boundary points using the MAT tangent plane(s) or vector(s) at the point.
The trivial MAT to boundary conversion case is when the MAT is comprised of a single point p = (x, y, z, r). In this case, the boundary is simply the sphere of radius r centered at (x, y, z). This follows immediately from the Envelope Property.
For a space curve MAT point p with a continuous tangent vector T (with respective projections p and T ), the related boundary has (double or finite) contact with a circle. This follows since if the MAT curve is given by (x(s), y(s), z(s), r(s)), and d is the direction vector connecting p to any related boundary point, then
where * is the dot product operator and u(d) is the unit vector in the direction d. Since T and r'(s) are fixed for a particular MAT point p, the angle alpha between T and d is constant, hence there are two circles which could be related to p, via their respective cone of distance. In Figure 2 these two circles are shown, with direction vectors of length r displayed in red.

Figure 2 : The 2 possible distance cones and related contact
circles.
A single circle is selected based on the sign of r'(s). If r'(s) > 0, then the boundary is increasing in the direction of traversal at p, so the circle with alpha < pi is selected, that is, angle alpha0 in Figure 3. If r'(s) < 0 then the boundary is decreasing in the direction of traversal, so the circle with alpha > pi is selected, that is, alpha1 in Figure 3. If r'(s) = 0, the two circles coincide with alpha = pi.

Figure 3 : Selecting the cone of distance based on the sign of r'.
Curve points with only a single one-sided tangent vector are analogous to end points in the two-dimensional case. Using the one-sided tangent, a related boundary circle is computed and, by the Envelope Property, the part of the sphere delimited by the circle and not intersecting the MAT must also be related to p. Again as in the two-dimensional case, three situations are possible. These are shown in Figure 4.
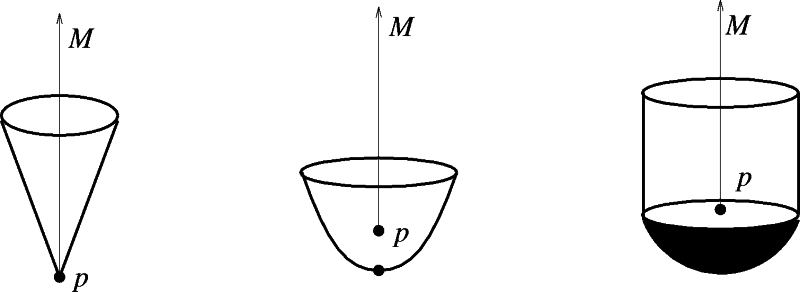
Figure 4 : Types of MAT end-points in 3D.
Finally, if p has two or more one-sided tangents, the related boundary is the intersection of the spherical caps obtained from each tangent vector taken individually.
A surface MAT point p with a well-defined tangent plane has exactly two related boundary points. These can be found by taking two linearly independent vectors in the tangent plane, computing the related circle for each as for curves, and finding the intersection of the two circles. In practice, this requires solving a system of three equations in three unknowns, two of which are (linearly independent) linear equations and the third of which is simply the equation of the unit sphere. Solving the system gives the two unit direction vectors, along which a translation of length r is required to obtain the boundary points.
An isolated singularity p in the MAT is required to have a parameterizable tangent space. Because of this, the direction vectors related to it can be found as the solution of a system of three equations in four unknowns. In general, the system has two curves as solution, but one of the solution can also degenerate into a single point. Figure 5 shows a conical MA with a tangent discontinuity at the apex and its related boundary. r values are assigned so that r = 0 around the base circle and increases linearly to 1 at the apex. The boundary related to the apex is the single point in the center of the base disc of the boundary, and the spherical cap on the top of the boundary, including the highlighted circle. Note that every other point of the MAT has exactly two related boundary points.
 |
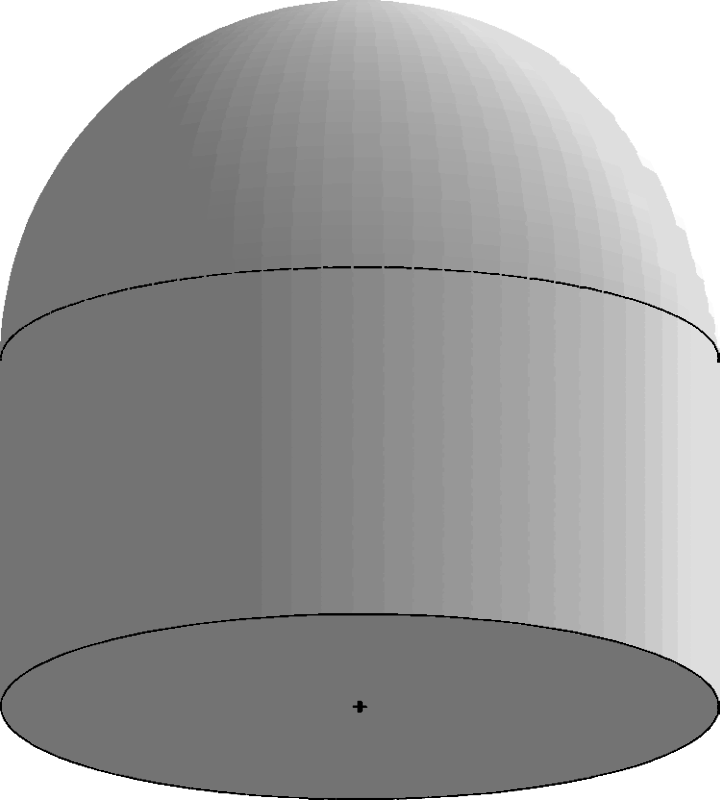 |
A point p on a curve which bounds an MAT surface patch has one or more circular arcs related to it. If p is on a single bounding curve and has a continuous tangent vector, it has one related circular segment. This segment connects the two surfaces which lie on either side of the MAT surface the curve is bounding. Taken as a whole, the bounding curve has as related boundary a sector of the generalized cylinder which would be related to curve if it were an MAT alone. The sector is determined by the tangent planes to the surface adjacent to the curve. Corners of the surface patch, where two or more curves meet with a tangent discontinuity, have in general a spherical patch as related boundary. Curves which are adjacent to two or more surface patches have the same number of cylindrical sectors related to them as the number of adjacent surfaces. Note that these sectors may degenerate into curves.
The final points of the MAT to be considered are points at which a space curve MAT and a surface patch MAT meet. By our assumption about such points on the MAT, if p is a joining point, it must be an endpoint of a curve segment c, and therefore there must be at least a circle related to c on the boundary. Now the only type of MAT surface point which could possibly have a entire circle on the boundary related to it is one at which the boundary surface has a spherical patch related to the MAT point. The surface MAT points which can have spherical patches related to them are points of tangent discontinuity, either isolated singular points in the interior of a surface patch, or points of tangent vector discontinuity on a bounding curve. Thus if p is of type P II, it must be tangent discontinuous as a component of the surface patch MAT.
In practice, to reconstruct the boundary points related to p, one need only find the boundary points related to p as a surface MAT point and find the circle C bounding the spherical patch related to p as a curve MAT point. Then the region on the spherical patch related to p as a surface MAT point which contains C is truncated by C. If the circle from the c at p matches exactly the boundary of the spherical patch from the surface MAT, then only the circle remains as the related boundary in the region. All other boundary regions related to p as a surface point remain unchanged.
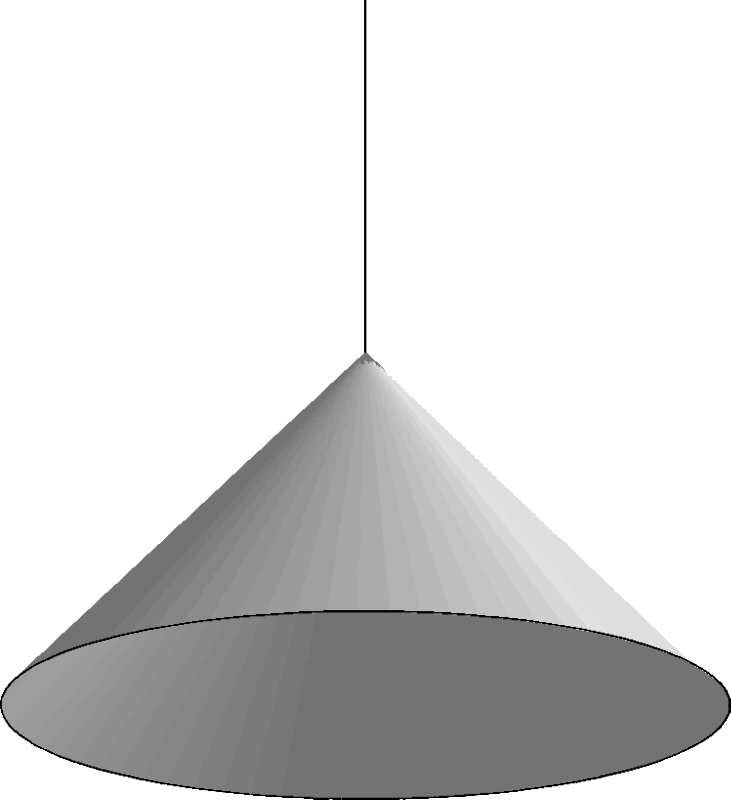 |
 |
 |
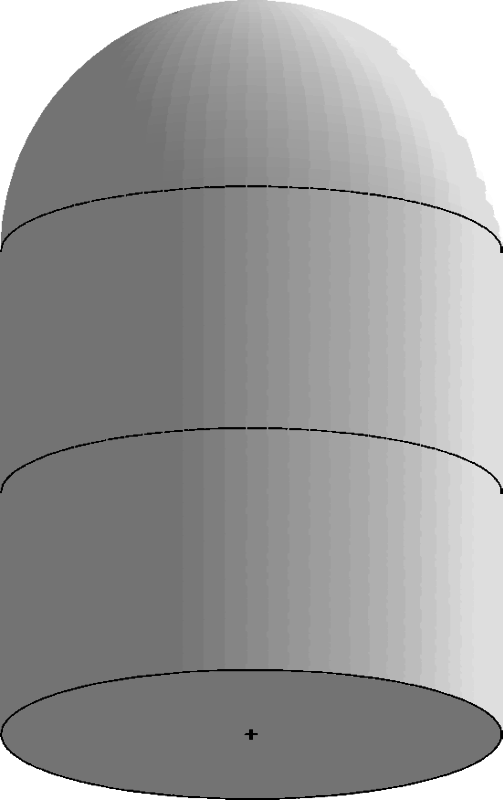
Consider the earlier example for isolated surface singularities, where the MAT had a singularity at p = (0, 0, 1, 1). If the line segment (0, 0, 1 + t, 1), 0 <= t <= 1 is added to this MAT, the boundary circles related to the surface and the curve segments would match exactly, and the boundary related to p would be the circle between the top and bottom silo sections shown in the middle of Figure 6. The spherical region on top is related to the MAT point (0,0,2,1), and the middle section of the silo is related to the line segment of the MAT between z = 1 and z = 2. The new MA is shown on the left in Figure 6.
If instead a line segment along the z-axis of length sqrt(2) is added, and the radius function made to decrease linearly along that line from a value of 1 at (0, 0, 1) to 0 at (0, 0, 1 + sqrt(2)), then the two boundary circles from the cone and from the line segment are no longer identical, hence the boundary related to p in this region of the MAT is the intersection of the spherical patches between the two bounding circles. This is shown in the rightmost figure of Figure 6. The cone on the top of the silo is the boundary related to the region of the line segment between z = 1 and z = 1 + sqrt(2). In neither case is the single boundary point related to (0, 0, 1, 1) on the opposite side of the MAT from where the line segment adjoins the MAT affected.