Programmoire + The Workstation
a combinatorial method for magic squares by Batool Desouky
Introduction
Programmoire engages with a mathematical artefact, the magic square, applying to its inherently computational logic a sorting algorithm that parses through all its permutations. Working with combinatorics and magic squares creates a new method for making magic squares, which, traditionally use more spatial algorithms for construction. The work is also informed by the tradition of making grimoires, which are textbook style compendiums of instructions on creating magical objects and cast spells. Programmoire takes the practice of recording elements, recipes and rituals and augments it into a programmable processes.
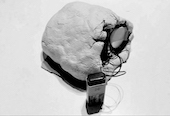
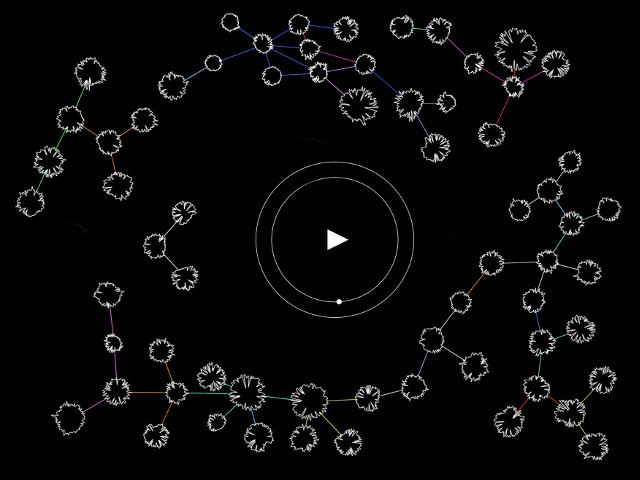
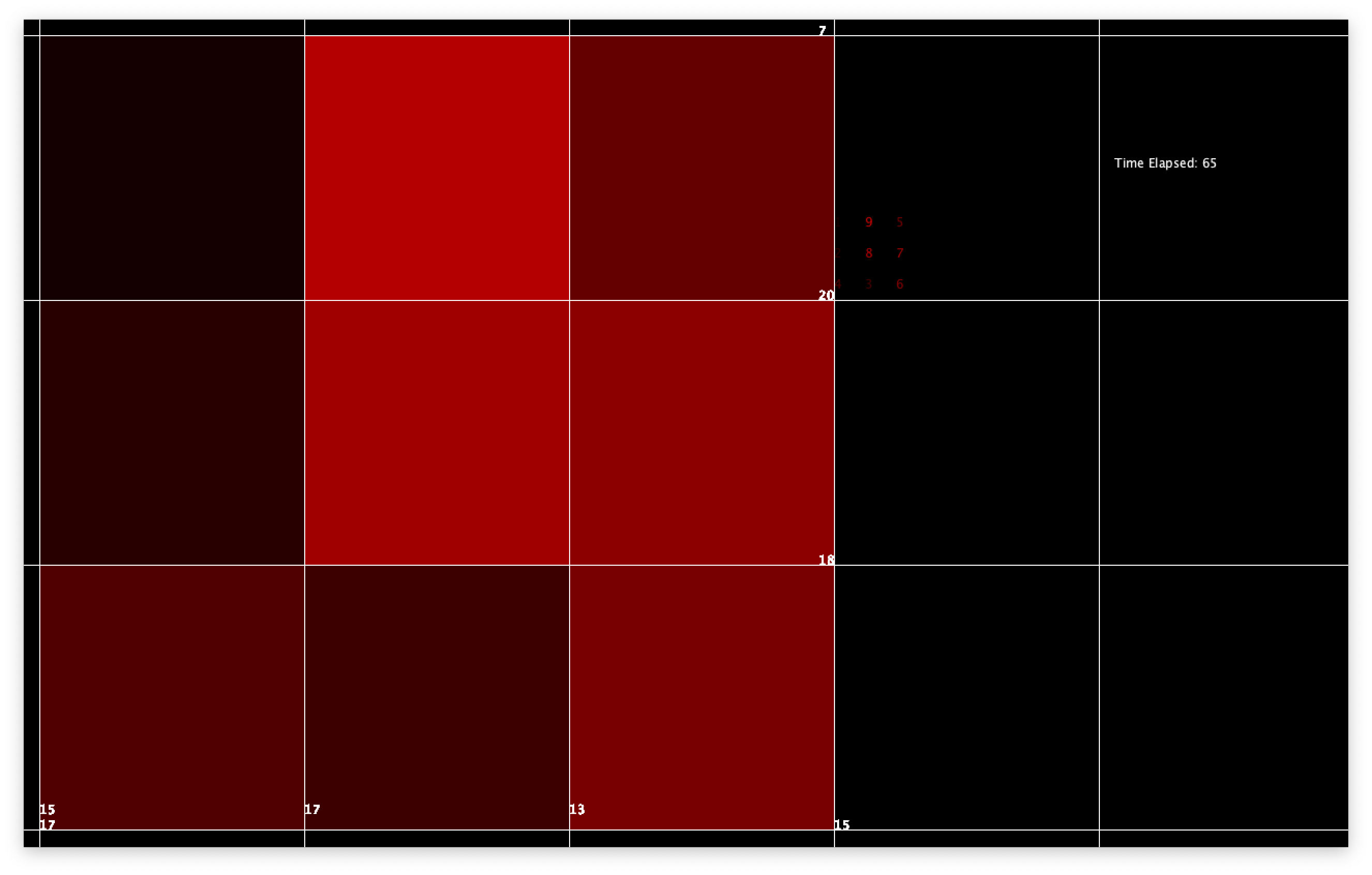
The installation presents a printed range from Programmoire in a bound book, as part of a workspace titled The Workstation. The Workstation displays the process of generating the permutations, through two screen displays and a live thermal printer, all mounted on a wall in front of a desk. One panel displays the live programme running through the number sequences and interfacing with the printer to outputs some of the corresponding sigils. The smaller panel displays a 3D rendition of the of the same process, alongside a 3D model of one of the magic Squares.
As a whole, the project explores the interchangeable associations between computation and magic., highlighting the intentional, procedural and executable within magic, to discuss the practice outside how it has been traditionally assigned as mystical, fleeting and unpredictable.
Concept and background research
I set out to create a combinatorial method for constructing magic squares, as an extension of my work with combinatorics in the past and applying them to narratives to create alternative timelines. [link to this project here]
The process of creating high-level “meaning” through an exercise of associating symbols with external [ideas] has always been fascinating to me. This process happens in code when assigning values to variables and functions to symbolic syntax, in language when assigning ideas and meanings to the letters and words, and in magic when assigning cosmic relations/power to sigils and talismans.
Of the many symbolic practices in magic, these squares are the most procedural and mathematical. They were also some of the first structures to which combinatorics was applied. They lent themselves quite naturally for my research as they stood at the intersection between computation, meaning, and magic.
Historical Research:
magic squares have been known and studies for centuries[1], they’re a historical object of fascination that acquired many uses. On a technical level, my research involved reading some of the translations of the early mathematical manuscripts [2] on the squares as a way of incorporating their history as an important background to the field of recreational mathematics which they are now a part of. These studies came prior to the talismanic uses of the squares, which were developed in later centuries and resulted in the transmission of magic squares from west Asia to Europe and also gave them their current English Language name. Before this point, the squares were referred to as The Harmonic Disposition of Numbers [3].
Technical Research:
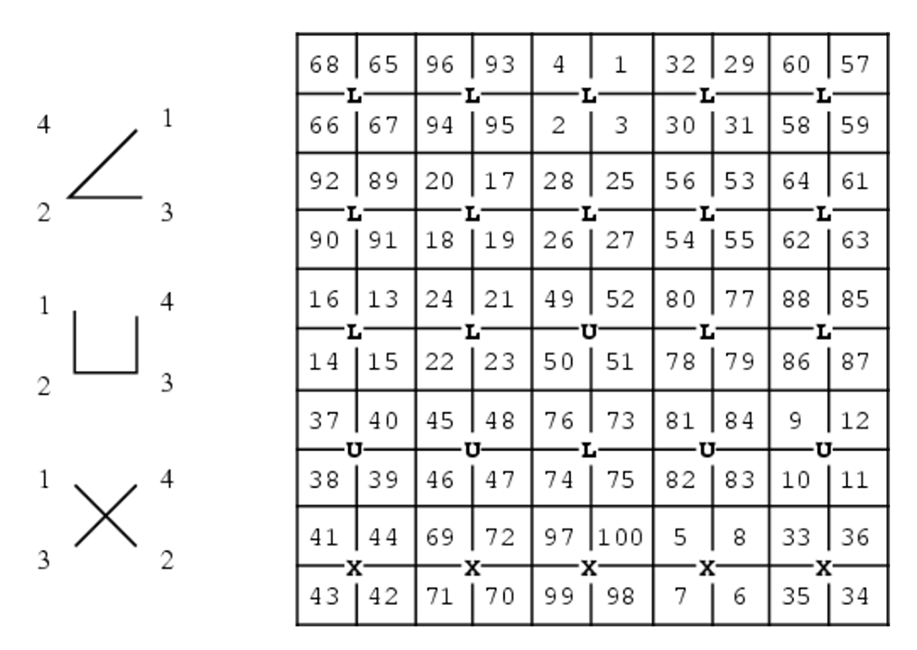
More recent work has been done on magic squares as part of recreational mathematics, the most notable of which is John Conways development of a new construction method for creating them, called the LUX method [4].
Construction methods are formulaic instructions on how to lay out numbers in a grid so that they create a magic square. There are many classifications of magic squares, the two that I explore in my projects are the basic or normal magic square, and the semi-magic square. Here is the criteria for each”
Magic Squares:
- Form a continuous string of the first n natural numbers, where n is the number of rows/columns, and also called the “order” of the square.
- The numbers cannot repeat
- Rows must add up to the same number that the columns add up to
- Diagonals must also add up to the same number
- It can be rotated, or reflected in any direction and still considered the same square.
Semi-Magic Squares hold the same relations as the above with the exception of the diagonals not having to adding up to the same constant.
All construction methods assume a 2D plain on which you can arrange and transform the matrix of the square in order to achieve the correct mathematical alignment. These methods are usually made for a human to execute, seeing as a spacial awareness is readily available to humans and which allows for the manipulation of elements on a surface easily.
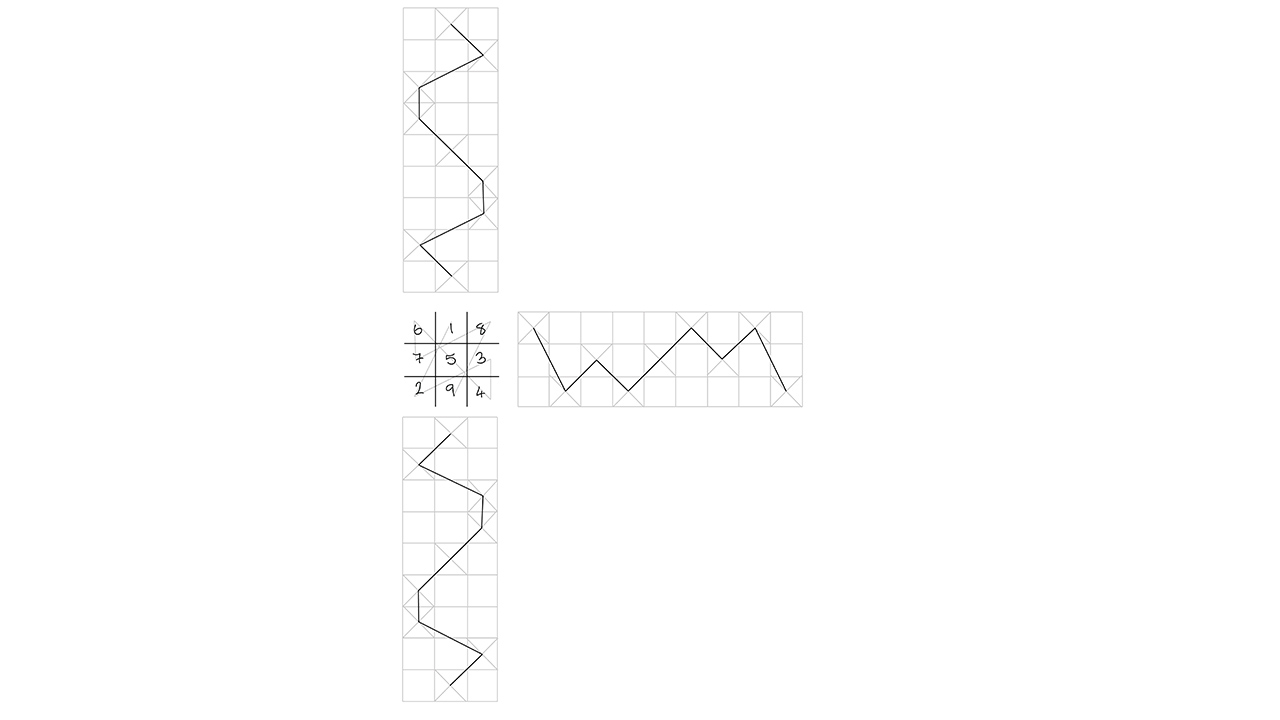
I wanted to explore doing this in a way that was more intuitive to digital code, treating the screen of a computer as a human-aid to help us see what the code is “thinking”. For this purpose, combinatorics was very useful and allowed me to work with the square as a string of data instead of an object in space.
Artistic Research:
I took inspiration from the practices of artists who worked with combinatorics and systems art in general, as well as artists who have specifically worked with magic squares.
Different artists have worked with magic squares to different effect; Emma Kuntz and Agnes Martin, have both worked with them as a reference to create harmonious, geometric visuals. Both their practices have an ethereal sense and draw on concepts of mysticism and healing [5]. Though I was not using them for visual effect per se, I found the concern for harmony very important and relevant to their associations with magic.
John Conway’s work with the squares was primarily a mathematical study, whose focus was on devising new and easier ways for achieving magic squares. His work was very important for grounding what I was doing as a “construction method” helping me define it as an exploration of process more than it was a visual exploration.
The images below are a photo I took of the Serpentine exhibit of Emma Kuntz work, and a screen shot on John Conways method from this page: https://archive.lib.msu.edu/crcmath/math/math/m/m029.htm
Technical
Technologies:
To create the printed part of Programmoire, I used a processing code to generate the permutations of the square based on a lexicographical ordering code borrowed from here [6]. I built a ‘bookmaker’ around this code to output .svg files of layers of different parts of each page of the book. I then used an Axidraw plotter to trace the .svg files to create each page of the book.
To create the installation, I had set out to design it as a workspace and to make it look more intimate or personable that an art installation usually would. At the same time, I didn’t want to break the illusion that this was a fictional space, so did not want to put a laptop or too many identifiable objects from the “real world”. As a result, I ended up loading my programme onto a raspberry pi and decided to go for a more lo-fi aesthetic to create this more intimate feel. I had printed some magic and semi-magic squares on the thermal printer to include in the installation to show some examples of what the code produces because waiting for it to reach the correct alignments in real time would have left the wall looking quite bare for a while.
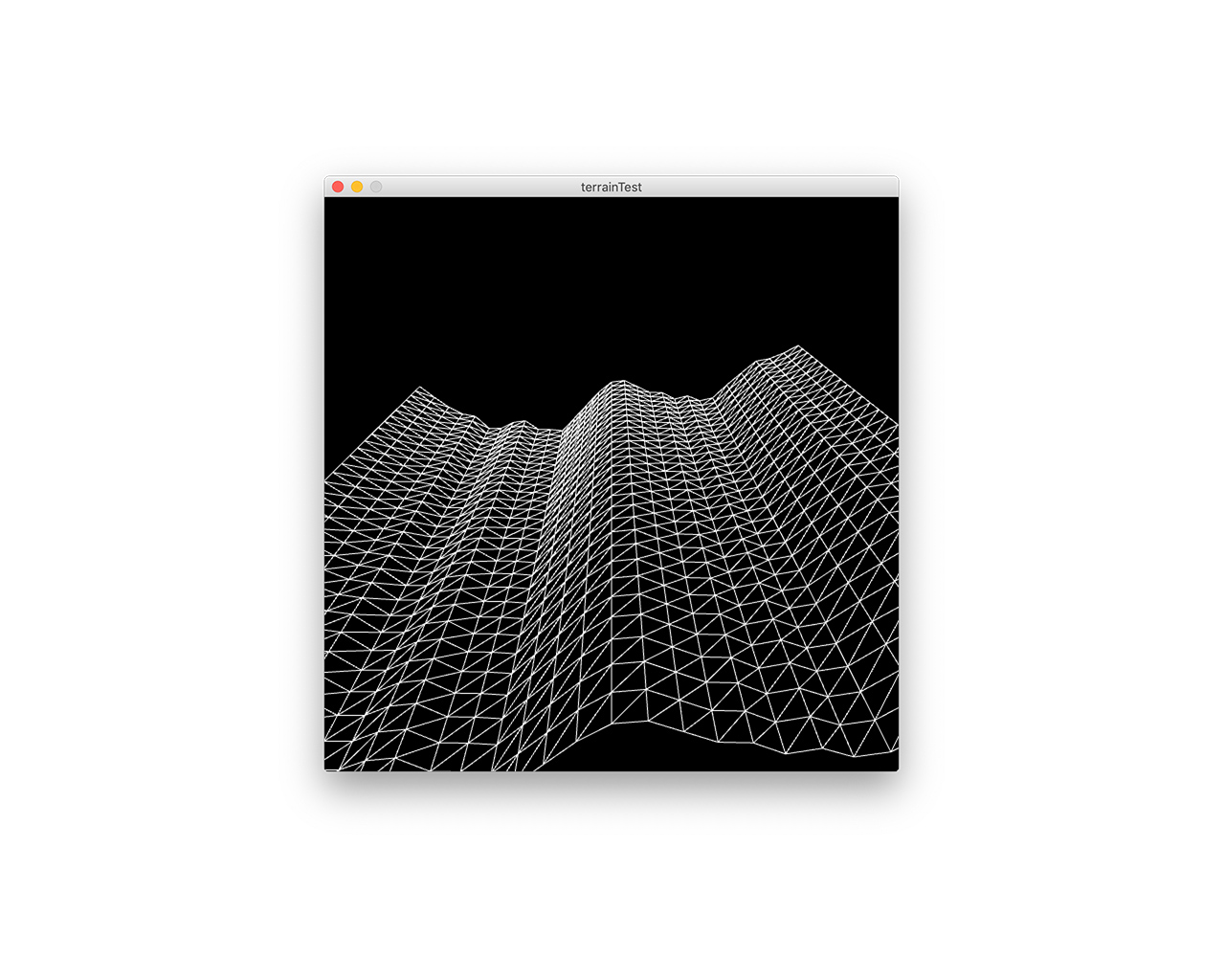
The installation space was meant to expose the process of creating the above, and also display some of the other explorations into the squares that did not make it into the prints, like the dimensional flattening and extruding of the shapes, and the durational aspect of the process in general. For the smaller screen, I had used the same code to extrude the shapes along the z axis, exported it into Fusion 360 to manipulate and put back in to the code to display on that screen. This was not very successful, and I’ll go into it in the self-evaluation section below.
Design and Formal Decisions:
As I was working between both digital and physical mediums and methods, I wanted to carry over the some of the logic from each into the other. Using a plotter allowed me to retain the more human act of drawing each shape and preserving the linear quality of the numbers. At the same time, I have been working on a screen for the most part of creating this piece and wanted to translate some of that format into the paper. Therefore, I cut the sheets of the book to a 6:10 aspect ratio to mirror that of the laptop screen I generated the shapes on. The final size of the book was a result of compromising between the standard A3 size of the Axidraw and the ratio of a 6:10 screen.
For the installation, I left the wires and circuit boards exposed though tried to create a visually pleasing aesthetic using them. I painted the wall to create a warmer feel and move away from the art-space white walls. I also created panels for the circuit boards, which were painted with pearlescent blue/violet paint and mounted using metallic golden screws to the wall. For the desk I mounted a black board of wood on top of a desk table to keep the colours in the space dark, and also try to obscure the identifiable object of the table.
Below are screenshots of some early prototypes of the code, an experimentation of applying it to create a terrain, and some digitised sketches.
Future development
The natural progression for the printed component of Programmoire is to print more of it! I used a friend’s Axidraw to print this part of the piece, and would love to create more of the prints into a heftier, denser data object.
For exhibition purposes, I would like to also present the live printing through the plotter as opposed to or alongside the thermal printer, though the printer was fitting as a prototype creator.
On a more digital level, I would like to host all the permutations of the programme on a website, and also create a virtual ritual space to explore the construction methods using a digital body and potentially other remote participants.
Self evaluation
At this stage I see this presentation of the project as a proof of concept of many of it’s components. I think the printed element of the work was very successful and that choosing to display the elements of the work in a workspace style installation was very fitting for the nature of the project.
However, some of the technical components were not very successful. The 3D part of project felt stunted and underdeveloped, and it was due to a complication with getting processing to export OBJ files. The grey 3D object seen in the installation (on the right of the small screen) was based on the code but was not actually produced by it. Also, I had aimed to create a 3D print from the model, but did not manage to learn how to use the water soluble PLA for printing supports for a structure like this. This is the biggest of the piece for me, because it would have largely added to the physical space to see some sculptural representations of what was in the book.
Working with a durational piece that a lot of time was spent cycling through the code to see if it works. Had I planned my time better I would have liked to be able to run the code for a full cycle in the space to see where in its progression I should start it so that it is more likely to produce prints during exhibition time.
References
[1] Yoke, Ho. Magic Squares in China. Encyclopaedia Of The History Of Science Technology And Medicine In Non-Western Cultures, Ed. Selin, Helaine, Springer Refernce, 2008, pp. 2598-2600.
[2] Sesiano, Jacques. Magic Squares In The Tenth Century: Two Arabic Treatises By Anṭākī And Būzjānī. Springer International Publishing, 2017.
[3] Comes, Rosa. “The Transmission of Azarquiel's Magic Squares in Latin Europe.” Medieval Textual Cultures: Agents of Transmission, Translation and Transformation, Ed. F. Wallis, R. Wisnovsky, De Gruyter, 2016, pp. 159-198.
[4] Walkington, William. "John Horton Conway And LUX". Carresmagiques.Blogspot.Com, 2020,
https://carresmagiques.blogspot.com/2020/04/john-horton-conway-andlux.html.
[5] Ellsworth, Angela. "Disembodied States: Walking The Magic Square". Open Space, 2020, https://openspace.sfmoma.org/2016/05/disembodied-stateswalking-the-magic-square/.
[6] https://github.com/CodingTrain/website/blob/master/CodingChallenges/CC_035.2_LexicographicOrder/Processing/CC_035_2_LexicographicOrder/CC_035_2_LexicographicOrder.pde
Further References:
Cramer, Florian, 2005. Words Made Flesh, Ed. Matthew Fuller. Piet Zwart Insitute.
Mauss, Marcel, et al, 2001. A General Theory of Magic. Routledge.
Bennett, Jane. Vibrant Matter a Political Ecology of Things. Duke University Press; Combined Academic [Distributor], 2010.