Recursive Reality - Projection Mapping
My Workshops in Creative Coding projection mapping final project. This project attempts to draw a lineage between computational art and art history through an exploration of the line.
produced by: Tate Smith
Discussion
My projection mapping project was framed around an attempt at summation of what I’ve learned on the course in just a few months of coding. It attempts to connect historical conceptions of art with computational art. The project is also an act of creative discovery; my own artistic processes never stem from the end goal of the project backwards. In this way this project was an exercise in a sort of “de-conceptualization,” wherein I had to approach my creative process from the opposite end. Thus, my project can be seen to both comment on historical discourses and conceptions of art as well as to further my own conception of how to begin the creative journey.
The first section, Lines, deals with the most simple of objects to manipulate in my experience thus far--the humble line. It is also an attempt to draw a lineage with canonical art history in order to create a linkage between the ultra contemporary field of computational art, which can feel disconnected from capital A art due to its inherently different mode of production, to the storied past of art. In order to situate myself within this history, I chose to work with “the line.” Famously in 19th century France Jean-Auguste-Dominique Ingres and Eugene Delacroix, two prolific artists of the time, represent two opposing sides of a dichotomous and contentious debate in art: the line versus the contour. Ingres steadfastly bore the standard for the line, while the deeply passionate Delacroix represented the latter. In this way the choice of working with the line was to cast my vote onto the team of the line and thus to continue a dialogue through the centuries. The shrinking form of abstract shape is a metaphor for the reduction that the artist, Ingres in this instance, would have to undertake the challenge of choosing what is important to represent in order to capture the image.
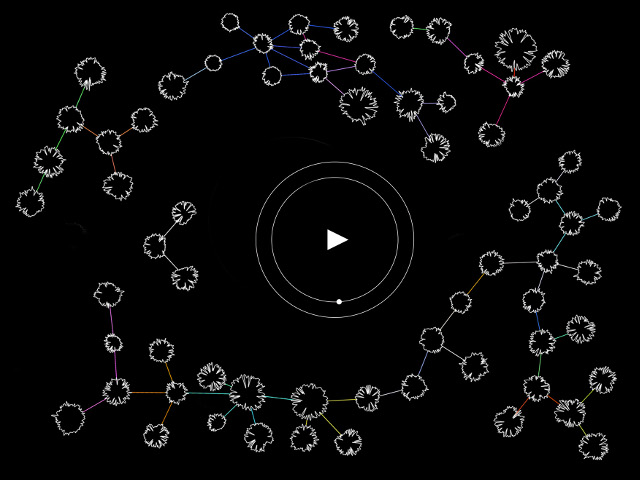
The second section focuses on recursion. This section acts as the crescendo to the piece through syllogism of the line piece and the relationship of computation art history. While the line piece sought to make an explicit connection to the larger scope of art through a specific visual language, the recursive piece makes its comment in a reflexive, recursive way. Similarly made up of lines, recursion alludes to itself as per the definition of recursion. This section seeks to deduce that all art is in itself a reference to art’s past. The idea of the artist as someone who pulls ideas out of thin air is old hat--art made today is not made within a vacuum, it always references backwards. In this light the recursive section comments on these conditions of art making with radical vulnerability accepting the self-referential nature of creating art past the age of mechanical reproduction, in an era of infinite reproducibility.
The final section, titled Spinning, acts as a sort of coda to the previous two sections. The purpose of this section is to suggest that the way forward is to spin our conception of art on itself. This section synthesizes the previous sections lines and recursion as a point of departure to conclude the piece.
Self evaluation
I believe my project was a success. It sought to explore broad topics through simple means. From this perspective I think this project was a success albeit it does only touch upon these things in a metaphorical sense. Overall, I am happy with the resulting imagery I created and the things I was able to generate. Our group worked very well together and our shape was exciting to make and fun to map.
In hindsight I wished I had used a diverse set of media, such as editing a video or image, as opposed to using only generated forms for my project. Furthermore, I wish I had taken better advantage of the underlying shape in my project; the tilted cube offered a unique opportunity for creating the illusion of 3 dimensions of which I wish I had better explored. While my projections utilized the shape effectively, I do not feel that they gained that extra "special-ness" from being projected on the cube and thus if I were to re-do this project I would have designed it for the cube more explicitly.
References
https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-8365.00241
I modified https://www.openprocessing.org/sketch/61047 by Eric Fickes to create the shrinking shape in the first section of my project.