The above video represents the artefact from the research of Morphogenesis using a series of edits from running the Gray Scott Model of Reaction Diffusion. (Ref 22)
01 Introduction
The development of a philosophy and algorithms surrounding Morphogenesis in art and design has been a recent historical event. The first documented events date back to the early empirical work of Frei Otto (ref 1), a German architect. Otto started his long journey into the study of biological growth and mechanisms in 1962 in Berlin. In contrast to this early non-computational work in architecture it has had a exponential growth and usage in contemporary architecture with the advent of faster and faster computers. Examples of contemporary morphogenetic structures are: The Orquideorama Botanic Garden,Eden Project Multiple, Spanish Pavilion at Shanghai 2010 to Selfridges Department Store (ref 2)
The use of the word Morphogenesis has been used in a variety contexts and meanings. Some have argued the basis of using the term dates back to Karl Marx in Capital (ref 3) and to the philosophical work of Gilles Deleuze in difference and repetition (ref 4) this will be reviewed below. On a scientific note Alan Turing (ref 5) was the first mathematician to postulate that the morphogenesis of a cell may well be based on the diffusion mathematics of different chemicals made by so called morphogens. (ref 6)
In the field of generative art the relatively recent work of Jonathan McCabe in his paper Cyclic Symmetric Mutli-Scale Turing Patterns (ref 7) descibes the generative work based on Turing’s equations that were based on the generative work of Greg Turk (ref 8). The reaction-diffusion equations that Turing describes in his paper can create a surprisingly rich range of complex patterns, with remarkable resemblance to many of those seen in nature such as pigmentation patterns on the coats of leopards, zebras and angelfish. This in turn has inspired the work of Andy Lomas in his paper Cellular Forms: an Artistic Exploration of Morphogenesis (ref 9).
Finally, I propose from the implementation of my artefact that the disciplines surrounding Morphogenesis need to be brought together under one umbrella to fully understand and utililise Morphogenesis.
fig 01 The Manuel Gea González Hospital cleans the air around it


02a Frei Otto
Frei Otto is our first example of a creative in design using Morphogenesis. A pioneering German Architect. We will look at two of his experiments:
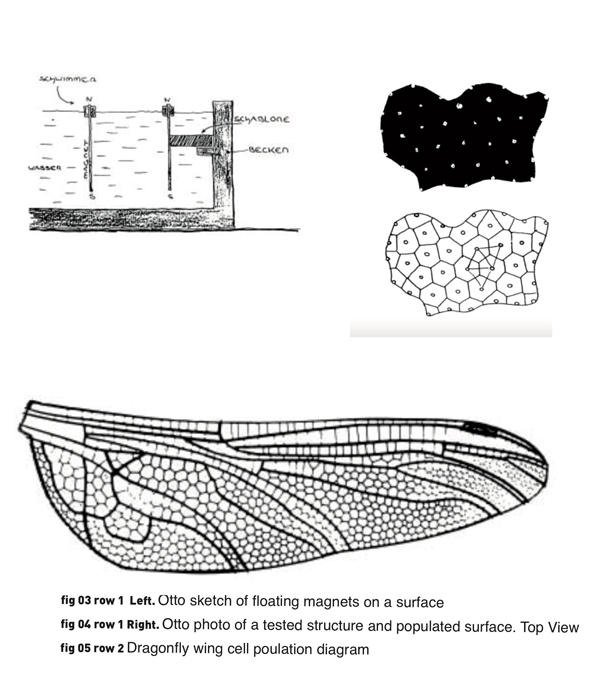
Frei Otto was the father of ‘form finding’ in architecture: using natural morphogenesis techniques to inspire his own architecture creations. He was one the first people to realize the power of morphogenetic design. The first experiment looks at a natural distance experiment using a defined limited surface area with a set of natural floating points that all use repulsive magnets to set there distance. (See Figure 03.) The boundary of the surrounding points make formations where the distance is the least to the surrounding neighbours. Forming shapes of hexagons and pentagons. (See Figure 04.) We can see a similar pattern arising in the distribution of the cells of a dragonfly wing. (See Figure 05.) The density of the cells changes so as to give greater strength and flexibility for the wing. But the principles of the underlying distribution are the same. And the cell shape is either four, five or six sided. Otto’s equal distance structure is still valid but with varying degrees of different magnetic forces, therefore some magnets will be packed closer than others.
The second experiment looks at Otto’s bubble shape surfaces when various defined areas of shapes are drawn through soap film. Distributing the shapes of the film in different ways.
See the following short films of his experiments.
https://youtu.be/-IW7o25NmeA
https://youtu.be/Gb5p0htTj4U
https://youtu.be/degls4ve_Dc
Figures 03 04 05

02b Frei Otto
The second experiment looks at Otto’s bubble shape surfaces when various defined areas of shapes are drawn through soap film.
Otto observed that given a set of fixed points the soap film will spread naturally between them to offer the smallest achievable surface area. These and other results from his experiments (shown in the above links) were the premise for work on the Munich Olympic Stadium. In 1974 the German-born civil engineer Horst Berger (working in the US) came up with the mathematics that allowed this process to be translated into the building structure of the Munich Olympic Stadium.(See Figures 06 07 08).
According to Otto, architectural processes should propose a methodology where generative structural issues are symbiotically organized in order to show a clear morphogenetic structure (ref 12). This is important as this process involves the presence of algorithms that modulate the structural form that were based on his empirical experiments. Consequently, his form becomes the result of a method of generative integration that takes into account form, hierarchy, as well as the structural manifestations of them.
Figures 06 07 08


2c Biomorphic Architecture
The next design examples of Morphogenesis are of Biomorphic Architecture that exhibit clear algorithmic mimicry or aesthetic mimicry.
Contemporary architectural examples are Bosjes Chapelin South Africa, Herzog and de Mueron’s 2008 Olympic Stadium in Beijing, Aqua Tower in Chicago, Kunsthaus Graz . All of these designs introduce computerized generative designs as opposed to Otto’s empirical experiments.
Biological structures contain morphogenetic properties in the way of repetition in which form, structure and chemical composition are not understood as pre-existing identities, they are reactive through dynamic generative interactions. The example of the Beijing National Aquatic Centre (See Figures 09,10,11) has been used to show how the process of geometric biomimicry can be integrated into the design of a large assembly building by means of modularity and repetition. It has geometric modules which are also found in other natural systems such as crystals, cells and molecular structures.
In 1887, Lord Kelvin proposed that the tetrakaidecahedron was the best shape for packing equal sized objects together to fill a space with minimal surface area. This shape was based on foam packing. Kelvin proposed a foam, based on the bitruncated cubic honeycomb, which is called the Kelvin Structure. However, Weaire–Phelan discovered another solution in 1993, the outer wall of the Aquatic Centre is based on the Weaire–Phelan Structure, (ref 13) a structure devised from the natural pattern of bubbles in soap lather.
John Bilmon of PTW Architects (the Watercube designers) said that: “The Watercube concept is a simple and concise square form that ultimately uses the water bubbles theory to create the structure and building cladding, and which makes the design so unique. It appears random and playful like a natural system, yet it is mathematically very rigorous and repetitious.”
Using the Weaire–Phelan Structure, the shapes that emerges are based on a set of 3D packing proposals that exhibit a minimal surface area. A very rigid rule in nature where the stress values on a structure are the least for a stable solution.
See Figures 09,10,11


03a Marxian Philosophy
The introduction and use of Philosophy into the structure of Morphogenesis is a recent event and relates to the work of lecturer and author Manuel DeLanda
(ref 17).
Let’s review the philosophy of difference spoken of by Karl Marx:
Human labour-power in its fluid state, or human labour, creates value, but is not itself value. It becomes value in its coagulated state, in objective form. The value of the linen as a congealed mass of human labour can be expressed only as an ‘objectivity’, a thing which is materially different from the linen itself and yet common to the linen and all other commodities.
- Karl Marx (ref 03)
What Marx means by this is that human labour creates ‘value’ through the morphogenesis of raw materials. The concept of the differential is perpetually at work as it is one of the necessary elements in the value-relation. (In short, for value to be produced, there must be relations of exchange and difference.) There must be a difference between the commodities for value to emerge.
Even though human labour has morphogenetic qualities when the whole system of human labour relations is looked at as a system itself it effects and changes the humans as well. For example, the computer, the mobile phone, the internet might be the result of human activity, yet when these formed multiplicities come to populate the world, humans in turn are formed differently as a result of their transformation of the environment.
There is thus a morphogenesis, a process of individuation, through which exchange-value is produced as an effect. This effect is the result of a transformation of a multiplicity into a specific form through labour.
The relationship between design and the Marxian theory of a coagulated shape is in the reference to transformation and the idea that a differential (in a design case a differential of calculus is a valid difference and a valid example could be a reaction-diffusion algorithm) is best used to see a true emergent state arise. It is the key to seeing a transformation process that brings about new patterns or shapes arising.
A design example of this is shown in Figures 12 and 13 taken from Alan Sanderson “Advanced Reaction-Diffusion Models for Texture Synthesis,” paper.
Figures 12 and 13


03b Deleuzian Philosophy
How does Marx labour difference philosophy tie into a more contemporary philosophy and usage with regard to Morphogenesis?
They tie in as both see "difference" and "differentials" as the key to value and change of an entity. “Difference is not diversity. Diversity is given, but difference is that by which the given is given, that by which the given is given as diverse." - Gilles Deleuze (ref 14)
This remark, which is not at all isolated in Deleuze’s work, suggests that difference, far from being equated with the actuality of what is given as Bruce Baugh (ref 15) would have it, is instead that which accounts for the actuality of the thing. In short, difference is the principle by which the given is given or produced, and not the given itself.
This claim undermines the central tenant of classical empiricist thought (David Hume) in its most basic essence, empiricism is a thesis about the origins of our knowledge and ideas. Hume expresses this point with great clarity in A Treatise Concerning Human Nature, “we shall content ourselves with establishing one general proposition, that all our simple ideas in their first appearance are derived from simple impressions, which are correspondent to them, and which they exactly represent.” Deleuze’s work is contrary, empirical identities by active synthesis is itself the result or product of differential passive syntheses.(ref 16)
If we again reflect on design and on an algorithm where the "difference" is the key component in its being then the work of Karl Simms a Boston based artist reproduced another differential example of difference by using the Gray-Stokes diffusion model and produced a variety of examples deign and emergent patterns formed by the algorithm. (See Figures 14 and 15.)
These patterns are showing the philosophy of difference as there driving force. Difference is the principle by which the given is given. It is a constantly evolving system through which we get an appreciation of emergence of shape and pattern arising.
Figures 14 and 15


03c Deleuzian Philosophy
Why are the ideas of Deleuzian Philosophy integral to the design process in Morphogenesis?
They are integral as Morphogenesis can be described as using a driving force algorithm with repetition of variation (a LaPlace convolution).
Deleuze states that: “Everything which happens and everything which appears is correlated with orders of differences: differences of level, temperature, pressure, tension, potential, difference of intensity.” Gilles Deleuze (ref. 14)
Thus, when we look at the symbiotic relationship between form, materials, structure and program, we should properly examine what causes differentiation among those levels, and how form consequently emerges. DeLanda (ref. 17 a lecturer and author) looks at three core principles derived from Deleuzian ideas of difference which he thinks should be considered when creating a generative morphogenetic process. He calls them: Population thinking; Intensive thinking; Topological thinking. (ref. 17b)
Population thinking. Any population of variable replicators coupled to any filter gives you an evolutionary process. For example, the gene pool with x and y chromosomes each have their own values of distinct features which each pair off to form new replicators and so the process repeats. The same process exists in genetic algorithms. Evolution is an automated search space of possibilities of process, in Deleuzian terms Repetition from the replicators and difference from the variable.
Intensive thinking. Intensive thinking drives process. Deleuzian intensive properties are density, speed, temperature and pressure. Intensive processes drive form, at very specific values of difference different forms materialize. Critical points of intensity called phase transitions define different stages in biology. Deleuze sees these properties as morphogenetically charged.
Topological thinking. In Deleuzian terms the differential is a driving process for morphogenes. Non-Euclidean geometries were born involving differentials of space. Differential geometry is a non xyz Cartesian space, they form topological spaces and represent forms of possibilities, a Deleuzian attractor of morphogenesis.
Another design example that has encompassed this style of using genetic style of algorithms (and that uses the ideas of repetition and difference and change is with Sterling Crispin installation Data-Masks, that uses genetic alogrithms to adapt and create machine vision maks of the human face. (See Figures 16,17 and 18.) The algorithms rely on genetic algorithms to make a formation of a mask. Data-masks are face masks which were created by reverse engineering facial recognition and detection algorithms. These algorithms were used to guide an evolving system toward the production of human-like faces.
Figures 16,17 and 18.


03d Deleuzian Philosophy
Population thinking; intensive thinking; topological thinking suggests the existence of a process whose modes of morphogenesis are inherently characterized by analogous genomic sequences. Using genetic algorithms to make designs.
A further design example of a genetic algorithm installation with variation would be United Visual Artists, Blueprint . (See figure 19 and 20.) This is an installation designed to explore the relationship and parallels between natural and artificial systems. With cells literally transferring their genes to their adjoining others, colour flows like paint across the canvas.
DeLanda’s methodology of complexity suggests the adoption of a analysis and understanding of morphogenetic changes that might explain the emergence of particular models of architectural production and assembly. Having these ideas as foundations of the algorithm. A replicable population with variation that has an intensive process driving the emerging results. Emergence of patterns formed from a simple agent within a complex system and patterns arise out of a multiplicity of relatively simple interactions.
Deleuzian understanding of systemic correlations of differentiations generates a new domain where emergent methodological design frameworks can be finally seen through a Deleuzian philosophy. This process is the combination of other interdisciplinary fields,such as biology, mathematics and chemistry all of which address the intricate structure of cellular organisms. Sometimes, this process involves looking at simplified geometrical diagrams of organic and compound forms that explain the existence and perhaps the emergence of particular patterns of form, structure and material. (The Laplace algorithms of chemical diffusion (Figure 21) are seen as a simplified matrix of surrounding cells feeding into the central cell.)
This approach requires the usage of differentiated mathematics in morphogenetic processes. We interpret these as a series of instructions which when constructed from an array of cells that form results which hopefully make unique and distinctive generative types. This then leads on to the mathematics that drives differencce to form.
Figures 19, 20


04a Alan Turing
Differentiated mathematics and morphogenetic processes. If we approach the use of the Morphogenetic process by including the ideas of DeLanda (spoken of above) then using a driving force of differentiation would be the optimum premise behind any generative art form. The most used has been an algorithm devised by Alan Turing. See Figure 21.
Alan Turing published a paper in 1952, The chemical basis of morphogenesis (ref 5) on the spontaneous formation of patterns in systems undergoing reaction and diffusion of their ingredients. Turing devised a mathematical model that explained how random fluctuations can drive the emergence of pattern and structure from initial uniformity.
Turing speculated that among the molecular ingredients of this bundle of cells are components called morphogens (‘shape-formers’), which are somehow responsible for triggering the development of a cell or tissue along a certain pathway. More specifically, a morphogen is a signalling molecule that acts directly on cells to produce specific cellular responses depending on its local concentration.
In his paper he assumed a particular geometric arrangement of cells in which the morphogens move and interact. For the sake of simplicity he chose to study a circular ring of cells and also a grid.
Greg Turk’s paper Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion (ref 8) showed how an implementation of Alan Turing’s equations can lead to a variety of simple and complex patterns.(See Figure 22.) These equations were further researched by artist Jonathan McCabe in his paper Cyclic_Symmetric_Multi-Scale_Turing_Patterns (ref 7) whereby different simulations were added together as multiple copies of the simple model (as a weighted sum, with the possibility of negative weights), operating simultaneously at different scales on the same data. (See Figures 23 and 24.)




04b Science and Artists
The relationship in Morphogenesis between the Artist and Scientists has been very close. (Figures 22 to 25 are Artists work and Figures 26 to 28 are both)
A different way of combining Turing’s patterns of multiple scales (rather than simply adding them together) is to switch between Turing’s instabilities of different scales at different time steps. Shown in Figure 25. Some of the resulting patterns have a marked resemblance to either animal patterns such as the leopard and angel fish. In 2008, biologists Akiko Nakamasu and Shigeru Kondo of Japan’s Nagoya University conducted experiments on fish and proved that the markings were corresponding with Turing equations. See Figure 26 and 27. Nakamasu and Kondo’s paper Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation (ref 18). Also PK Maini at Oxford University in his paper Two-stage Turing model for generating pigment patterns on the leopard and the jaguar (ref 19) showed how to simulate the patterns on leopards and jaguars.
Another artist working in this area is Andy Lomas (ref 20) and he has based his research on the division of cells. When the nutrient level in a cell exceeds a given threshold the cell splits into two, with both the parent and daughter cells reconnecting to their immediate neighbours. (See Figure 28.) Andy Lomas’ algorithm although similar in nature relies on the concentration to trigger the advent of a new particle and is 3D as well. The Turing code could also work in 3D. The number of scientific papers using Turing code is increasing as more scientists start to prove the validity of the paper in different fields of science. I think this will have an impetus upon artists wishing to explore the algorithm and the new and unusual ways the different artists can utilise it.
Due to the mathematical complexity of the diffusion equation there is not an abundance of generative artists working in the field, also the way of expressing the work thus far has been very linear, just iteratively playing with the parameters. However, it does lends itself to a interactive installation something more playful than Karl Simms’ Reaction-Diffusion Media Wall in Boston (ref 21). It is also part of the Deleuzian family of replicators and lends itself to both artistic and a genetic algorithm implementation. I would also assert that the algorithms can be hacked to generate more playful results whereby the viewer is controlling where and how the algorithm is implemented.
Another key point in using population and variation algorithms in generative art is that they have obstensibly fallen into two catagories: genetic algorithms with a driving alogrithm or just a driving alogrithm with the genetics built into the algorithm. The are both equally complex. However, the latter type have a close relationship with science.
Figures 26 27 and 28


05a Artefact
By playing with a reaction diffusion equation I learnt a number of things.
I have designed an artefact of an implemented diffusion alogrithm. Different animated test results can be seen in the following link and also example stills are shown in figure 29:
https://youtu.be/kiE6Vt-nUMU (Same video as at the beginning of the paper)
My artefact consisted of a implemented interactive diffusion equation algorithm based on the Gray-Scott model (Ref. 22). See Figure 31. The user is able to dynamically control the algorithm by clicking to add more “cells” and by dragging the mouse to change the feed parameter (F) and the kill parameter (k).
All of the processes are inherent in the algorithm that DeLanda spoke of (Ref. 17) a process that has both repetition and variation which is controlled by user interaction. There is a partnership between the user and the algorithm by means of the mouse. There is an exploratory understanding of what it means to both “kill” a chemical and to “feed” it these are intrinsic processes controlled by a diffusion rate and they are topological by using a Laplace transform. Difference defines the algorithm from which emerges the patterns.
There is an emergence behaviour within the algorithm to form complex patterns. These arise out of a repetition of relatively simple interactions.
Figures 29 and 31:




06a Conclusion
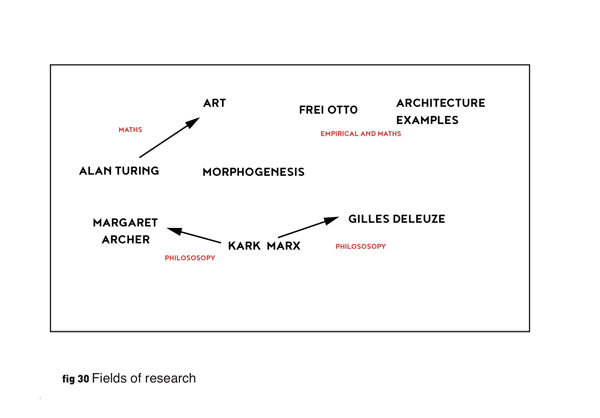
In reference to Figure 30 I have looked at the surrounding fields of research: architecture, philosophy, science and art. Frei Otto was the first artistic pioneer of Morphogenesis using an empirical palette of documented test results that were accrued from different test parameters and were performed as a series of repetitions of experiments documenting the morphogens of different materials, from magnetic fields to soap film. As Manuel DeLanda says in his lecture “Deleuze and the Use of the Genetic Algorithm in Architecture” (ref 23) he entered into a partnership with the natural world of Morphogenesis using surface tension as a structural form to create a new form of architecture.
This is what DeLanda sees as “the productive use of genetic algorithms implies the deployment of three forms of philosophical thinking (populational, intensive, and topological thinking) which were not invented by Deleuze but which he has brought together for the first time and made the basis for a brand new conception of the genesis of form” He uses the Deleuzian philosophy of Repetition and Difference as a ground work to build his Morphogenetic work upon (using population,intensity and topology thinking). Using Reaction Diffusion algorithms as a source of this kind of thinking we have seen both scientific merit and some artistic endeavours using similar algorithms. In modern architecture only a few recent structures use the algorithms of building a form that are actually Morphogenetic as most seem to mimic the process.
Figure 30

06b Conclusion
Throughout the process of working on my artefact I understood the powerful emergent qualities of morphogenetic generative algorithms. This way of working can create a wealth of possibilities, captivate an audience and also has meaning. There seem to be a lot of different algorithms to explore (any differential physical process can be used) and when looking at Jonathan McCabe and Andy Lomas’ work we see very different outcomes.
In conclusion, moving forward I would like to see Morphogenetic design in all its different science and art forms becoming multi disciplinary. Currently, this is not the case particularly with philisophy as only DeLanda is disseminating this area. To solidify the work of different exponents of the Morphogenetic field I would propose the creation of a conference with the aim to get together all practitioners and combine the fields of science, art, architecture, philosophy and empirical studies into a new identity for Morphogenesis.
I assert that what DeLanda has done so far in combining the philosophy of Deleuze with genetic algorithms in architecture is pioneering an expansive way of collaborating in the Morphogenetic field. However, we can go further by also including generative artists and scientists from such fields as biology into the equation. This would also mean combining more empirical work coming from the field of science, this is important because it was an inherent philosohy in Frei Otto’s work. Otto believed in the partnership of natural Morphogenesis as as aid in the design of new architecture. By involving more themes and perspectives into the consideration of what Morphogenesis means we would be able to expand the field of Morphogenesis to its full potential. Something I believe both Frei Otto and I would welcome.
I also propose generative artists move towards a practice of form-finding in their work (as Frei Otto did) as an inspirational tool and also help in forming new ideas. That would involve a series of playful experiments involving the physical properties of different materials. The experiments need not be completely scientific. The outcome would be to help integrate the artist within a natural biomorphic environment to help seed the artist into a similar mind set and feed his/her creativity.
Moreover, the artists are encouraged towards a practice in which they collaborate with science or scientists in utilising some of the experimental models they use in there experiments and pushing the work further on in different directions. (Andy Lomas work (ref 9) encompasses this kind of aesthetic.)
I feel architectural practices work within a “extraction model” of the results they seek in nature. Rarely do they partner with scientists. I feel this is a big mistake. Partnership of any kind that goes outside your own practice is always more beneficial and perhaps useful to others. An artist who uses a science algorithm outside of the original confines of its defined use can also inspire the scientist to think outside their own area of research.
One of the most interesting results in utilising a reaction diffusion algorithm is that you can’t predict the outcome in terms of the work you will produce. You become the sideline of the work. The non-human agent (the algorithm) becomes the centre of the work. I find this reassertion of the machine as a Artist to be a equally fascinating area of research. As is the case of my own artefacts. The algorithm is not within our visual grasp of the results: the complexity mirrors our reality. I also propose the agency of the Nonhuman Turn can be also added on into the pholosophy of Morphogenesis and our understanding of this subject.


INTRO:
1.”Frei Otto.” Wikipedia. March 19, 2018. https://translate.google.co.uk/translate?hl=en&sl=de&u=https://de.wikipedia.org/wiki/Frei_Otto&prev=search Frei Otto Short History. At the Technical University of Berlin, he founded in 1961/62 with the biologist Johann-Gerhard. Helmcke, the research group biology and construction.
2. Duran, Virginia. “10 Examples of Biomorphic Architecture.” Virginia Duran Blog. April 25, 2017.
https://duranvirginia.wordpress.com/2012/12/27/curiosities-10-examples-of-biomorphic-architecture/
3.Reuten, Geert. "The difficult labor of a theory of social value: metaphors and systematic dialectics at the beginning of Marx's Capital." Marx’s Method in Capital: A Reexamination(1993): 89-113. Page 9.
https://www.researchgate.net/profile/Geert_Reuten/publication/318542532_The_difficult_labour_of_a_theory_of_social_value_metaphors_and_systematic_dialectics_at_the_beginning_of_Marx%27s_Capital/links/596f9741a6fdccc6c96c117b/The-difficult-labour-of-a-theory-of-social-value-metaphors-and-systematic-dialectics-at-the-beginning-of-Marxs-Capital.pdf
4. Deleuze, Gilles. Difference and repetition. Columbia University Press, 1994. https://en.wikipedia.org/wiki/Difference_and_Repetition
5. “The Chemical Basis of Morphogenesis.” Wikipedia. March 03, 2018.
https://en.wikipedia.org/wiki/The_Chemical_Basis_of_Morphogenesis.
http://www.dna.caltech.edu/courses/cs191/paperscs191/turing.pdf
6. “Morphogen.” Morphogen - Wikipedia.
https://en.wikipedia.org/wiki/Morphogen
7. McCabe, Jonathan. “Cyclic symmetric multi-scale Turing patterns.” In Bridges Conference, pp. 24-28.2010.
http://www.jonathanmccabe.com/Cyclic_Symmetric_Multi-Scale_Turing_Patterns.pdf
8. Turk, Greg. “Generating textures on arbitrary surfaces using reaction-diffusion.” In ACM SIGGRAPH Computer Graphics, vol. 25, no. 4, pp. 289-298. ACM, 1991. https://dl.acm.org/citation.cfm?id=122749
https://www.google.co.uk/urlsa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0ahUKEwjHjZvk7b7ZAhXBa1AKHchhCcMQFggsMAA&url=https%3A%2F%2Fwww.cc.gatech.edu%2F~turk%2Fmy_papers%2Freaction_diffusion.pdf&usg=AOvVaw2zstfkKileyn37CrnysTQG
9. Lomas, Andy. “Cellular forms: an artistic exploration of morphogenesis.” In SIGGRAPH Studio, pp. 1-1. 2014.
https://www.google.co.uk/urlsa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&uact=8&ved=0ahUKEwiY05eA7r7ZAhWOYlAKHaddD6cQFgg0MAI&url=http%3A%2F%2Fwww.andylomas.com%2Fextra%2Fandylomas_paper_cellular_forms_aisb50.pdf&usg=AOvVaw16p-ot1UodmI6AwjtNjeNY
10. Thompson, D. W., and Arcy Wentworth. “On growth and form, 1917.” Cambridge [Eng.]: University press. xv (1970). https://en.wikipedia.org/wiki/On_Growth_and_Form
ARCHITECTURE
11 Otto, Frei. "Occupying and Connecting: Thoughts on Territories and Spheres of Influence with Particular Reference to Human Settlement" Edition Axel Menges, 2009.
https://www.amazon.co.uk/Occupying-Connecting-Territories-Particular-Settlement/dp/3932565118
12. Otto, Frei. “Finding Form: Towards an Architecture of the Minimal”, Edition Axel Menges (19 Jan. 1996)
https://www.amazon.co.uk/Finding-Form-Towards-Architecture-Minimal/dp/3930698668
13. “Weaire–Phelan Structure” - Wikipedia. https://en.wikipedia.org/wiki/Weaire–Phelan_structure
PHILOSOPHY
14. Deleuze, Gilles. Difference and repetition. Columbia University Press, 1994 Page 280 and Page 222. https://en.wikipedia.org/wiki/Difference_and_Repetition
15. “French Hegel: From Surrealism to Postmodernism” Routledge; 1 edition (3 July 2003) https://books.google.co.uk/books?isbn=1317827724
16. “Gilles Deleuze (Stanford Encyclopedia of Philosophy).” https://plato.stanford.edu/entries/deleuze/
17. DeLanda, Manuel. “THE USE OF GENETIC ALGORITHMS IN ART.” https://cumincad.architexturez.net/system/files/pdf/acadia12_25.content.pdf
17B. DeLanda, Manuel. "Deleuze and the Use of the Genetic Algorithm in Architecture." Architectural Design 71, no. 7 (2002): 9-12.
http://crisisfronts.org/wp-content/uploads/2008/08/deluze_genetic-algorithm.pdf
ART
18. Kondo, Shigeru, and Takashi Miura. “Reaction-diffusion model as a framework for understanding biological pattern formation.” science 329, no. 5999 (2010): 1616-1620. http://science.sciencemag.org/content/329/5999/1616
http://science.sciencemag.org/content/329/5999/1616?sid=7d751fa0-7fa5-409c-842a-c38ab1b8dd26
19. Liu, R. T., S. S. Liaw, and P. K. Maini. “Two-stage Turing model for generating pigment patterns on the leopard and the jaguar.” Physical review E 74, no. 1 (2006): 011914. https://journals.aps.org/pre/abstract/10.1103/PhysRevE.74.011914
https://people.maths.ox.ac.uk/~maini/PKM%20publications/212.pdf
20 “#LumenInFocus: Andy Lomas.” #LumenInFocus: Andy Lomas - Lumen Prize.
http://lumenprize.com/blogpost/lumeninfocus-andy-lomas.
http://www.andylomas.com/extra/andylomas_paper_cellular_forms_aisb50.pdf
21 “Karl Sims Home Page.” Karl Sims Home Page. http://karlsims.com/. http://www.karlsims.com/rd-exhibit.html
ARTEFACT
22. “Gray Scott Model of Reaction Diffusion.” Gray Scott Home Page
https://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/
23. DeLanda, Manuel. “Deleuze and the Use of the Genetic Algorithm in Architecture.” Architectural Design 71, no. 7 (2002): 9-12.
http://crisisfronts.org/wp-content/uploads/2008/08/deluze_genetic-algorithm.pdf